MÁGNESSÉGTAN - ELŐADÁS ANYAG
Mozgási és nyugalmi indukció. Faraday-féle indukciós törvény.
Elektromágneses tekercs. Önindukció, Lenz-törvénye
Váltakozó feszültség és áram előállítása, teljesítménye. Elektromos energia átalakítása.
Váltakozó áram hatása alatt álló áramköri elemek Ohmos, kapacitív, induktív ellenállás
Elektromágneses Lorentz-erő
Mágneses Lorentz-erő a neve annak az erőtörvénynek, amely a mágneses térnek a v sebességgel mozgó töltésre gyakorolt hatását írja le:
(12.8)
A mozgó töltésre az elektromágneses tér hatását együttvéve a teljes Lorentz-erő írja le:
vektori alakban
(12.8)
Mozgási és nyugalmi indukció. Faraday-féle indukciós törvény.
Mozgási indukció
Az indukált feszültség nagysága: Ha egy l hosszúságú vezeték a mágneses tér irányára merőlegesen helyezkedik el és a hosszára és a mágneses térre is (amelynek mágneses indukciója B) merőlegesen v sebességgel mozgatjuk, a két végpontja között U feszültség indukálódik.
(m2.1)
Az indukált áram iránya: (Lenz - törvény): Az indukált áram iránya olyan, hogy mágneses hatásával akadályozni igyekszik az őt létrehozó változást (Ez megfelel az energia megmaradás elvének).
Tétel: Faraday-féle indukciós törvény: Az indukált feszültség (U) arányos egy tekercs menetszámával (N) és a mágneses indukció fluxus változási gyorsaságával (DF/Dt):
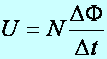(m2.2)
Elektromágneses tekercs. Önindukció, Lenz-törvénye
Def.: Önindukciónak nevezzük azt a jelenséget, amikor a saját mágneses fluxus változása miatt keletkezik indukált feszültség.
Az önindukciós feszültség (Ui) arányos az áramerősség változási gyorsaságával (DI/Dt) és a tekercsre jellemző mennyiséggel, az önindukciós együtthatóval (L).
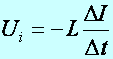(m2.3)
Tétel: A tekercs önindukciós együtthatóját geometriai adatok (N, A, l) és anyagi paraméter (mr) alapján is felírhatjuk, a tekercs mágneses energiája (Eelm) pedig a következő:
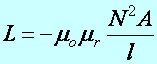(m2.4)
Tétel: A tekercs mágneses terének energiája:
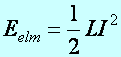(m2.5)
Váltakozó feszültség és áram előállítása, teljesítménye.
Def.: Váltakozó áramnak nevezzük az olyan elektromos áramot, amely iránya és nagysága periodikusan változik. Homogén mágneses térben az erővonalakra merőleges tengely körül egyenletes szögsebességgel forgatott zárt vezető keretben indukált elektromotoros erő:
(m2.6)
Tétel: A váltakozó áram effektív feszültségén, ill. effektív áramerősségén annak az egyenáramnak a feszültségét, ill. áramerősségét értjük, amely ugyanabban a vezetőben, ugyanannyi idő alatt ugyanannyi hőt fejleszt, mint az adott váltakozó áram.
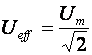
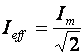(m2.7)
Tétel: A váltakozó áram munkája és teljesítménye:
(m2.8)
Az elektromos energia átalakítása. A transzformátor feszültség átalakító berendezés, a terheletlen transzformátor primer és szekunder feszültségei úgy aránylanak egymáshoz, mint a primer és szekunder menetszámok:
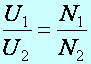(m2.9)
A feszültség feltranszformálásával az áramerősség letranszformálása jár együtt (energia megmaradás elve).
Váltakozó áram hatása alatt álló áramköri elemek
Def.: Ohmos ellenállásnak nevezzük azt az áramköri elemet, amelyen váltakozó áram esetében is a kapocsfeszültség fázisban van az áramerősséggel. Jele: R
Def.: Induktív ellenállásnak nevezzük egy tekercsnek az önindukciója miatt a váltakozó árammal szemben fellépő ellenállását (a tekercsen a kapocsfeszültség fázisban 90o –os szöggel siet az áramerősséghez képest) Jele: XL:
(m2.10)
Def.: Kapacitív ellenállásnak nevezzük egy kondenzátornak a kapacitása miatt a váltakozó árammal szemben fellépő ellenállását (a kondenzátoron a kapocsfeszültség fázisban 90o –os szöggel késik az áramerősséghez képest) Jele: XC:
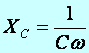(m2.11)
Eredő feszültség, impedancia. Teljesítménytényező.
Tétel: Sorba kapcsolt ohmikus, induktív és kapacitív tagokból álló hálózatban (soros RLC körben) az egyes kapcsolási elemeken eső effektív feszültség értékekre (UR, UL, UC) a vektori összeadás művelet érvényes. Így az effektív kapocsfeszültséget (Uk) az előző tagokból a következő összefüggés alapján lehet kiszámolni:
(m2.12)
Def.: Váltóáramú ellenállásnak, más szóval impedanciának nevezzük az effektív kapocsfeszültség és az effektív áramerősség hányadosát, amely egy állandót szolgáltat:
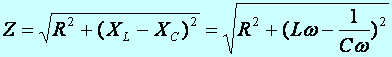(m2.13)
A fáziseltolódás szögét a következőképpen lehet számítani:
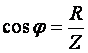
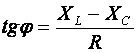(m2.14)
„Hatásos” (Joule-hőt fedező) teljesítményt csak az ohmikus ellenálláson ad le az áramkör:
(m2.15)
Váltakozó áramkörben az effektív teljesítményt a következő összefüggés alapján lehet számítani (cosj, fázistényező):
(m2.16)
Háromfázisú áram. Generátorok, erőművek.