Alapvető ismeretek félvezetőkből álló áramköri elemekről

Félvezetők hőmérséklet függése.

Áramvezetés fémekben

Volta féle kísérlet, az érintkezési feszültség.

A Peltier-hőhatás, hőelem. Seebeck-effektus

Alkalmazási területek, eszközök

 

Alapvető ismeretek félvezetőkből álló áramköri elemekről

 

Def.: Félvezetőnek nevezzük azokat a szilárd halmazállapotú, kristályos szerkezetű anyagokat, amelyeknek a fajlagos ellenállása a fémek és a szigetelők fajlagos ellenállása között van (10-5 Wm < r < 107  Wm). A vezetőképességük a hőmérséklettel exponenciálisan nő.

A legismertebbek a germánium (Ge) és a szilícium (Si). (Továbbiak: Se, CdS, PbS, PbSe, GaAs SiC,..). A utóbbi két évtizedben viszont nagyon nagy számban állítanak elő egyéb elemek kombinációjával félvezető kristályokat, amelyek meghatározó jelentőségűek a nagy frekvenciás- és az optoelektronikában.

 

Tranzisztorok, integrált áramkörök anyagai: A tranzisztorok, integrált áramkörök egykristályos, egynemű anyagból készülnek; többnyire szilíciumból. Az egykristályos szilíciumban adalékolással (három vagy öt vegyértékű anyag igen kis mennyiségben való hozzáadásával) különböző vezetési típusú zónákat lehet kialakítani. Az öt vegyértékű adalék atomok az elektronok feldúsulását okozzák, így jutunk az n típusú félvezetőhöz. A három vegyértékű atomok a lyukakat teszik dominálóvá, ez a p típusú félvezetőanyag.

 

Félvezetők hőmérséklet függése

 

A félvezető anyagok tulajdonságai erősen hőmérsékletfüggők, ellenállásuk csökken mivel a hőmérséklet emelkedésével nő a töltéshordozók koncentrációja. A félvezető anyagok ellenállásának hőmérsékletfüggése jól közelíthető egy exponenciális kifejezéssel (6.2. ábra):

            (e3.1)

 

ahol A a T = ¥ értékhez tartozó ún. maradék-ellenállás, és B > 0 a félvezető anyagára jellemző állandó (B = DE/k, ahol DE a félvezető tiltott sáv szélessége, k pedig a Boltzmann-állandó). A (2) kifejezés természetes alapú logaritmusát véve egyenes egyenletét kapjuk, amelynek tengelymetszetéből A, meredekségéből B meghatározható.

         (e3.2)

 

Ezen a jelenségen alapszik a termisztor, azaz a félvezetőből készült hőmérő.  

 

Áramvezetés fémekben

 

- Volta-féle kísérlet. Az érintkezési feszültség, termofeszültség

- Peltier-féle kísérlet, (Peltier-hőhatás és a hőelem) (termolektromos jelenségek)

 

Volta-féle kísérlet Az érintkezési feszültség (Alessandro Volta 1745-1825)

 

Kísérlet leírása: Elég sima felületű réz (Cu) és cink (Zn) lemezeket, a rájuk erősített szigetelőanyagból készült nyelénél fogva szorosan összeérintünk, majd gyors mozdulattal széthúzzuk egymástól. A lemezekre kapcsolat elektrométer feszültséget jelez. Két fém érintkezésekor az egyiknek pozitív, a másiknak negatív lesz ez eredő töltése töltése. Ezt a kísérletet mindenféle fémmel párosítva egymáshoz el tudjuk végezni. (Ez nagyon hasonlít az elektromos alapjelenségek során tapasztalt megosztás jelenségéhez.)

 

Kvalitatív értelmezés: A különböző fémek vezetési elektronjainak potenciális energia szintje egymástól különbözik. Szoros érintkezésekor, a köztük levő feszültség miatt elektronok áramlanak át az egyik fémről a másikra, aminek következtében az egyiken elektron többlet, a másikon pedig elektron hiány lesz, „konzerválva” a feszültséget. A fémeket és a fémekhez hasonló viselkedésű vezetőt, Az azonos feltételek mellett tapasztalt érintkezési feszültségek nagyságai alapján feszültségi sorba lehet rendezni. Kimérhető a Volta-féle feszültségi sor. A jelenség során két fém érintkezésekor annak lesz pozitív töltése, amelyik a Volta-féle feszültségi sorban megelőzi a másikat.

 

Termofeszültség, termoelem

Kísérlet leírása: Forrasszunk össze réz (Cu) és cink (Zn) huzalokat. A két szabad végre kapcsoljunk érzékeny (mV tartomány) feszültségmérőt. Tapasztalat: ha változtatjuk a forrasztási pont hőmérsékletét, változni fog az egyenfeszültség is. Egy ilyen összeállít

Kvalitatív értelmezés: A Volta-féle feszültség hőmérséklet függését tapasztaljuk. A két fém érintkezése során, az egyiken kialakult elektron többletet, a másikon pedig az elektron hiányt a hőmozgás befolyásolja.

Kvantitatív következtetés: Az két végpont között megjelenő feszültség arányos a hőmérsékletkülönbséggel:

              (e3.11)

 

ahol az indexben levő számok a termoelemet alkotó anyagokra utalnak. A lineáris közelítés szűk hőmérséklet-tartományban illetve kisebb pontossági igények esetén alkalmazható. Szélesebb hőmérsékleti intervallumban további állandók bevezetése szükséges.

Ezen jelenségen alapuló eszközt, mint hőmérőt, széles hőmérséklet tartomány (200-400 fok) alkalmazza az ipar és a háztartás.

 

A Peltier-hőhatás és a hőelem

 

Kísérlet leírása: Forrasszunk össze réz (Cu) és cink (Zn) huzalokat. Csatlakoztassunk az összeforrasztási helyhez hőmérőt (termoelem, termisztor). Kössük be az így elkészített összeállítást egy egyenáramú áramkörbe. Tapasztalat: ha a rézre kapcsoljuk az áramforrás pozitív sarkát (a cinkre a negatívot, tehát az elektronok a cink felöl haladnak a réz felé), akkor az összeforrasztási helyen melegedést tapasztalunk, ha a rézre az áramforrás negatív sarkát kapcsoljuk, az összeforrasztási hely hidegebb lesz, mint korábban volt, hőt von el a környezetéből.

Kvalitatív értelmezés: Ha a rézre kapcsoljuk az áramforrás pozitív sarkát (ekkor az elektronok a cink felöl haladnak a réz felé) Ha a vezetési elektronok mozgását külső elektromos térrel hozzuk áramlásba és az elektronok a rézből a cinkbe jutottak, energiaszintjük emelkedett, amelyhez az energiát a környezetükből vették fel. (forrasztási hely lehűlt). Fordított áramirány esetében az elektronok energiaszintje csökkent, energiát adnak le a környezetüknek, melegítik a forrasztási helyet. A termofeszültség jelenség és a Peltier-hőhatás jelenség fémek esetében egymás „tükörképei.

Kvantitatív következtetés: Az egységnyi idő alatt felszabaduló vagy elnyelt hőnek megfelelő hőteljesítmény (P_P) arányos az I árammal, ahol Q a hő, p a Peltier-együttható T az abszolút hőmérséklet.

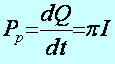                  (e3.12)

 

Ezen jelenségen alapuló eszközt, mint „hűtőberendezés” Peltier-elem néven ismert.

 

Seebeck-effektus

Kísérlet leírása: Összeépítünk egy np félvezető párt. Ha az np félvezető pár n-típusú tagjának kivezetése (A), és a p-típusú tagjának szabad vége (C) azonos hőmérsékletű (T_o), az összeépítés helyének (B) hőmérséklete pedig T, (T ¹ T_o) az A és C pont között U feszültséget mérhetünk.

Kvalitatív értelmezés: Az np félvezetőkből kialakított elrendezésnél tapasztalt jelenség, a fémeknél termofeszültség effektusként ismert.

Kvantitatív következtetés: Ez az effektusra jellemző az anyagtól és hőmérséklettől függő a állandót a következő egyenlettel definiáljuk:

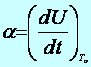          (e3.13)

 

Ha a fent leírt összeállításon áram folyik, az áram irányától függően a B pontban hő szabadul fel, vagy hő nyelődik el. Ezen jelenségnek a „fordítottja” is létezik, azaz félvezető összeállításoknál is tapasztalható a Peltier-effektus.