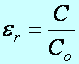ELEKTROMOSSÁGTAN - ELŐADÁS ANYAG
Elektromos alapjelenségek, kvalitatív leírásuk
Coulomb-féle erőtörvény, Elektromos töltés.
Elektromos erőtér. Elektromos térerősség vektor, feszültség.
Elektromos fluxus. Gauss tételek. Vákuum dielektromos állandó.
Kapacitás. Kondenzátor. Kondenzátorok soros és párhuzamos kapcsolása
Elektromos alapjelenségek, kvalitatív leírásuk
Tapasztalatok:
- műszálas inget a rajta levő műszálas pulóverrel együtt levetünk, majd
szétvesszük őket, szétválasztáskor vonzást mutatnak és még szikrákat is
tapasztalunk. Az erős vonzás lassan megszűnik. A ruhaneműk felvételével ez a
jelenség újból előidézhető
- népszerű csokoládés szeletről levesszük a nagyon vékony csomagoló anyagot,
amely „tapad” a kezünkhöz
- a televízió és a számítógép monitorjának képernyője hamarabb poros lesz
(pedig függőleges), mint a teteje
- felhők között, a föld és a felhő között nagy villámok jönnek létre, stb.
Kvalitatív leírásuk:
Testek elektromos állapotba hozása, bizonyos testek összeérintése, egymás dörzsölése és szétválasztása útján érhető el. Ezáltal testek között tudunk vonzást és taszítást „előidézni és megszüntetni”. Kétféle elektromos állapotba hozhatók a testek, így kétféle elektromos töltésről beszélünk. Ezek megkülönböztetésére, megnevezésére az 1700 évek végén a POZITÍV és a NEGATÍV szavakat vezették be.
Def.: Megállapodás szerint pozitívnak nevezzük egy testnek azt az elektromos azt az elektromos állapotát, amilyenbe az ebonit jut, ha szőrmével dörzsöljük meg, majd eltávolítjuk az ebonittól a szőrmét. (megjegyzés: a szőrme elektromos állapota ekkor negatív lesz).
Def.: Megállapodás szerint negatívnak nevezzük egy testnek azt az elektromos állapotát, amilyenbe az üveg jut, ha posztóval dörzsöljük meg, majd eltávolítjuk az üvegtől a posztót. (megjegyzés: a posztó elektromos állapota ekkor pozitív lesz.
Megjegyzés: minden más, nem fémes két test, felületének összeérintése, majd szétválasztása után, kisebb nagyobb mértékben a testeknél ugyanezt a kétnemű elektromos állapotot tapasztaljuk. Az „etalon” testekhez viszonyítva „bevizsgálhatjuk” azt, hogy milyen a „nemük”.
Tapasztalat, hogy kellően szoros érintkezésbe hozott testek elektromos állapotba jutnak, ami abban nyilvánul meg, hogy a korábbiakhoz képest erőt gyakorolnak egymásra. Az azonos nemű töltött testek taszítják egymást, az ellentétes nemű töltött testek pedig vonzzák.
Mai értelmezés: Az elektromos állapot kialakulását a modern fizika anyagszerkezeti magyarázata, az atomokról leváló elektronok egyik testről a másikra (a nagyon közeli felöleti érintkezés során következhet ez be) „átvándorlásával” írja le. Az elektron felfedezése után (1897) a makroszkópikus eredmény értelmezése a következőképpen szól: az a test lesz eredőként negatív, amelyikre rámennek a szabad elektronok, ugyanakkor a másik test pedig eredőként pozitív lesz, mert azon elektronhiány alakul ki.
Coulomb-féle erőtörvény. Elektromos töltés.
Az eredő elektromos töltéssel rendelkező testek között ható erő kvantitatív megadására a két pontszerű testre megállapított Newton-féle gravitációs erőtörvény nyújtott támpontot, a kiterjedt testek kölcsönhatásának leírására pedig szintén a tömegeloszlást is figyelembe vevő, térfogati integrálás alkalmazása volt sikeres már a XVIII század végén. Coulomb az általa, pontszerű testek kölcsönhatására megfogalmazott erőtörvény kísérleti „ellenőrzésére” az 1791-ben Cavendish által elkészített torziós ingának megfelelőt készített. Coulomb a következőképpen fogalmazta meg a nevével fémjelzett törvényszerűséget:
Tétel:
(Coulomb törvénye) Az (1-es) jelzésű pontszerű test által a
(2-esre) gyakorolt erő (![]() )arányos az 1-es (
)arányos az 1-es (![]() ) és a 2-es (
) és a 2-es (![]() ) test elektromos töltésével és fordítottan arányos a
köztük levő távolság négyzetével. Ennek az erőnek az iránya, azonos nemű
töltött testek esetében megegyezik 1-esből a 2-esbe mutató helyvektor (
) test elektromos töltésével és fordítottan arányos a
köztük levő távolság négyzetével. Ennek az erőnek az iránya, azonos nemű
töltött testek esetében megegyezik 1-esből a 2-esbe mutató helyvektor (![]() ) irányával. Az arányossági tényező jele (k), nagysága
pedig SI-ben a következő:
) irányával. Az arányossági tényező jele (k), nagysága
pedig SI-ben a következő:
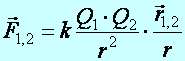 ahol
ahol
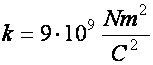 (e1.1)
(e1.1)
Megjegyzések: Az elektromos kölcsönhatás 41 nagyságrenddel nagyobb a gravitációs kölcsönhatáshoz képest.
Elektromos erőtér. Elektromos térerősség vektor, feszültség. Vákuum dielektromos állandó.
Az elektromos kölcsönhatás további leírására, a Faradaytól származó „közelhatás elvet” alkalmazzuk. Ez az az egységes elv, amelyet a gravitációs kölcsönhatásnál is alkalmazunk. Eszerint az elektromosan töltött test, elektromos hatását tekintve, folyamatosan csökkenő módon, a „végtelenig” hat, terjed és ahol a másik test van, annak a töltésére ott fog hatni. Ehhez a gondolkodásmódhoz ilyen fogalmakat kell bevezetni, mint az Elektromos erőtér. Az elektromos erőtér jellemzésére pedig lehet alkalmazni vektor (elektromos térerősség) és skalár mennyiségeket. Ezek a következők:
Def.:
Az elektromos térerősség (jele:
![]() ) vektormennyiség, a próbatestre ható erő (
) vektormennyiség, a próbatestre ható erő (![]() ) és a próbatest elektromos töltésének (Q)
hányadosával definiált fizikai mennyiség. Egysége: N/C (másképpen V/m):
) és a próbatest elektromos töltésének (Q)
hányadosával definiált fizikai mennyiség. Egysége: N/C (másképpen V/m):
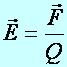 (e1.2)
(e1.2)
Def.:
Az elektromos feszültség (jele
![]() ) az elektromos töltésnek az A pontból a B pontba történő
mozgatása során végzett munka (
) az elektromos töltésnek az A pontból a B pontba történő
mozgatása során végzett munka (![]() ) és az elektromosan töltött test töltésének (Q) a
hányadosával definiált fizikai mennyiség. Egysége: J/C, röviden 1 V (Volt).
) és az elektromosan töltött test töltésének (Q) a
hányadosával definiált fizikai mennyiség. Egysége: J/C, röviden 1 V (Volt).
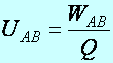 (e1.3)
(e1.3)
Def.: A tér bármely pontjának (P), egy kitűntetett ponthoz (O) viszonyított feszültségét, potenciálnak, U(P) nevezzük.
Nagy jelentősége lesz a későbbi leírásban a következő módon bevezetett mennyiségnek, a vákuum dielektromos állandójának
Def.:
A vákuum dielektromos állandója (eo)
a következő összefüggés alapján vezethető be:
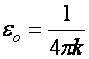
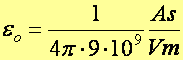 (e1.4)
(e1.4)
Elektromos fluxus. Gauss és Maxwell tételek.
Az előző megfogalmazásokból néhány további mennyiség és eredmény származtatható:
Def.: Az elektromos fluxus (jele Y) az elektromos térerősség (E) és a felület (A) szorzata által definiált fizikai mennyiség. Egysége: Vm.
![]() (e1.5)
(e1.5)
Tétel:
A pontszerű töltés (Q) elektromos térerősségét E(r), r
távolságban a következő összefüggés alapján számoljuk ki:
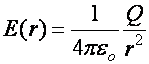 (e1.6)
(e1.6)
Az eddigi matematikai „tapasztalatokat” Gauss (1830), majd Maxwell (1858) a következőképpen általánosították, ezzel ezek a megfogalmazások a későbbi leírásaik axiómái lettek:
I.
Axióma:
Gauss-tétel, vagy Maxwell I.
törvénye: Zárt felületre az elektromos fluxus (Y)
egyenlő a bezárt össztöltés (SQ)
és a dielektromos állandó (eo)
hányadosával:
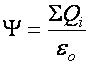 (e1.7)
(e1.7)
II. Axióma:
Elektrosztatika II alaptörvénye,
vagy Maxwell II. törvénye: Zárt görbe mentén a Q töltésen végzett
munka zérus, azaz két pont között mozgatott töltés esetében végzett munka
független az úttól.
![]()
![]() (e1.8)
(e1.8)
Megjegyzések:
A Maxwell I. szemléletes jelentése: az elektrosztatikus tér forrásos,
A Maxwell II. szemléletes jelentése pedig, hogy örvénymentes.
Az elektrosztatikus tér forrásai az elektromos töltések.
Anyagszerkezeti értelmezés: a negatív töltés hordozói az elektronok, a pozitívé pedig a protonok.
Kapacitás. Kondenzátor. Kondenzátorok soros és párhuzamos kapcsolása
Def.: Kondenzátornak nevezzük a két vezetőből és a köztük levő szigetelőből álló rendszert.
Def.:A
kapacitás (jele: C) (töltés befogadó képesség) a kondenzátorra
vitt töltés (Q) és a kondenzátor fegyverzetei közötti feszültség (U)
hányadosával definiált fizikai mennyiség. Egysége: C/V, röviden Farad.
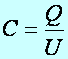 (e1.9)
(e1.9)
Tétel:
A síkkondezátor kapacitását geometriai adatok (A, d) és
anyagi paraméter (er)
alapján is felírhatjuk, energiája (Eel)
pedig a következő:
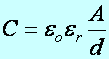 (e1.10)
(e1.10)
Tétel:
A síkkondezátor fegyverzetei közötti elektromos tér energiáját
a következő összefüggés alapján lehet kiszámolni:
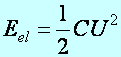 (e1.10)
(e1.10)
Tétel:
Soros (Cs)
és párhuzamos (Cp)
kapcsolás esetén az eredő kapacitás:
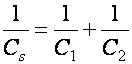
![]() (e1.11)
(e1.11)
Def.: A kondenzátorban alkalmazott szigetelő megnöveli a kondenzátor kapacitását (C) a vákuumbeli értékhez (Co) képest, ezt az arányt az illető anyag relatív dielektromos állandójának, vagy relatív permitivitásnak nevezzük (er):