Kepler-féle törvények. Bolygók mozgása. A Föld keringése a Nap körül.

A Newton-féle gravitációs erőtörvény származtatása.

Mozgások az inercia rendszerhez képest mozgó vonatkoztatási rendszerben műholdak..

Hullám függvény, terjedési sebesség kötélhullám, hanghullám

Laboratóriumi mérési gyakorlatok

 

Kepler–féle törvények. Bolygók mozgása. A Föld keringése a Nap körül.

 

I. törvény: A bolygók ellipszis pályákon keringenek, amelyeknek egyik gyújtópontjában a Nap áll (a numerikus excentricitás Föld esetében e = 0.017).

II. törvény: A Naptól a bolygókhoz húzott rádiuszvektor egyenlő időközök alatt egyenlő területeket (területi sebesség: dq/dt) súrol:

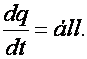         (d5.1)

 

III. törvény: A bolygók keringési időinek (T) négyzetei úgy aránylanak egymáshoz, mint az ellipszispályák nagy tengelyeinek (r) köbei (más megfogalmazásban: a keringési idő négyzetét osztva az ellipszispályák nagy tengelyeinek köbével, minden bolygóra ugyanazt az értéket kapjuk):

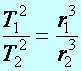            másképpen   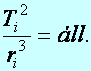      (d5.2)

 

 

ahol   i=1, 2,..9 (Merkur, Vénusz,…..Plutó)

 

A Földről indított műholdak sebesség értékei:

Első kozmikus sebesség:
                   8 km/s         ahol   g=9,81m/s2 R=6738 km (d5.3)

 

Második kozmikus sebesség

       11 km/s 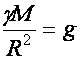         (d5.4)
Geostacionárius pálya 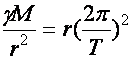      r=42000 km         (d5.5)

 

A Newton-féle gravitációs erőtörvény származtatása.

 

A Napnak a bolygókra gyakorolt hatását leíró erőtörvény származtatásának lépései a Newtoni mechanika elvei alapján a következőkben kerül bemutatásra. (mivel ennek a gondolatsornak, az általánosítással együtt, valamint a Cavendish-féle kísérlettel együtt, alapvető szerepe van az egész fizikát és az eddigi világképünket érintően, ezért ennek részletesebb bemutatása következik itt. Ennek lépései a következők:

1. Tapasztalat: Kepler III. törvénye a Nap Vénusz, Föld, Mars, Jupiter bolygók mozgásáról (helykoordináta-idő függvényéről).

2. Ebből kell kifejeznünk a bolygó mozgása során tapasztalt gyorsulását. Közel körpályán haladnak, tehát a TP kinematikája szerint gyorsulása „centripetális”. A centrumban a Nap „áll”, Ő a centripetális hatás ’kiváltója”.

3. Ha beírjuk a dinamika alapegyenletébe a bolygó tömegét és gyorsulását, megkapjuk a Nap által rá gyakorolt hatás erőtörvényét. (Newton III. axiómája szerint a bolygók is ugyanakkora erővel hatnak a Napra) (1686)

4. Ezután következik Newton általánosítása, hogy ilyen hatás minden test között „létezik”, csak a többi hatáshoz viszonyítva nagyon kicsi, ezért „nem tűnik fel”. A testek közötti hatás kimérésére nagyon extra berendezést kellett készíteni. Ez az elméleti „jóslat” után csak 110 év múlva realizálódott. A Cavendish az általa készített torziós ingával 1791 mérte ki a g értékét.

Részletes ismertetés:

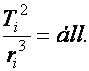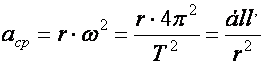
 Ţ

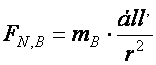 Ţ  Ţ 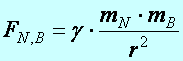 (d5.6)

 

Elméletileg, még „jósolni kell” arról, hogy egy kiterjedt test esetében a felszínétől „kifelé”, milyen távolságfüggést „sejthetünk”? Erre a kiterjedt homogén, gömb alakú testre történő, térfogati integrálást felhasználó számolás adja azt az eredményt, hogy a felszíntől „kifelé” a gravitációs hatásának távolságfüggése olyan, mint a tömegközéppontjába „képzelt”, azonos tömegű, pontszerű test hatása.

Ha az általánosítást elfogadjuk, akkor a Föld is ugyanilyen erőtörvény szerint hat a rajta levő, és a körülötte keringő testekre. A felszínén (r=R) a 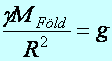 (d5.7) értéke kimérhető, g értékét a Cavendish-féle ingával történt mérésekből elfogadva a Föld tömegére kaphatunk értéket. A Föld térfogatát ismerve, pedig az átlagsűrűségét tudjuk számolni.

 

Mozgások az inercia rendszerhez képest mozgó vonatkoztatási rendszerben

Két vonatkoztatási rendszer közül az egyik a másikhoz képest ugyanúgy, mint az egyik tömegpont a másikhoz képest, végtelen sokféle formájú mozgást végezhet. Felmerülhet ekkor az a kérdés, hogy egy harmadik testnek az egyik és a másik vonatkoztatási rendszerhez viszonyított mozgása átszámítható-e.

A newtoni erőfogalmat ezidáig testek közötti kölcsönhatásban értelmeztük, tehát minden erőnek meg tudtuk adni az ellenerejét. Kérdés továbbá, hogy a mozgások dinamikai leírása (az adott pályán történő mozgás dinamikai feltételének megadása) azonos-e, vagy eltérő a két vonatkoztatási rendszerben.

Kérdés, hogyan alakul a gyorsulása egy testnek abban a vonatkoztatási rendszerben, amely egy másikhoz képest
1 egyenes vonalú egyenletes transzlációt végez,
2 egyenes vonalú egyenletesen változó transzlációt végez,
3 egyenletes forgó mozgást végez,

 

Az 1-es esetre a Galilei-féle relativitási elv a válasz.

Tétel: (Galilei-féle relativitási elv) (a klasszikus mechanika relativitási elve) Az egymáshoz képest egyenes vonalú egyenletes transzlációt végző koordináta rendszerek a mechanikai jelenségek leírása szempontjából teljesen egyenértékűek, ha az egyik inercia rendszer, akkor a másik is az. A dinamika alapegyenlete a Galilei-féle transzformációval szemben változatlan.

A Galilei-féle transzformáció:          x=x'+v t,

                                                     y=y'

                                                     z=z'                                                (d5.8)

                                                     t=t'.

 

Def.:  A 2-es esetben, az egyenes vonalban egyenletesen változó mozgást végző koordináta rendszerben a tömegpontra a korábbiakhoz képest egyetlen új erőt, az  transzlációs tehetetlenségi erőt értelmezzük, amely ellentétes a koordináta rendszer gyorsulásával.

Def.: A 3-as esetben, az egyenletes forgó mozgást végző koordináta rendszerben, ha a tömegpont nyugalomban van, rá már akkor is hat a forgástengelytől kifelé mutató (s) és attól s távolságban levő tömegpontra a centrifugális erő, , (d5.9) amely a forgás szögsebességének négyzetével arányos.

Def.: A 3-as esetben, ha a tömegpont az egyenletes forgó mozgást végző koordináta rendszerben v' sebességgel halad, rá további erő, a Coriolis-féle erő is hat , (d5.10) amely iránya merőleges a mozgás irányára és a forgástengelyre. A Coriolis-féle erő egyébként kielégíti a centripetálisság feltételét.

 

A következő táblázat foglalja össze ezeket az eseteket:

Tehetetlenségi gyorsulások	Nevük	Tehetetlenségi erők
	transzlációs tehetetlenségi
	centrifugális
	Coriolis

 

A fentiek alkalmazásával a következő tapasztalatok arra utalnak, hogy a gömb alakú Föld forog a tengelye körül:
- a nehézségi gyorsulás függ, azonos tengerszinti magasság mellett attól, hogy milyen szélességi körön vagyunk (sarkokon g=983,2 cm/s2, egyenlítőn g=978,0 cm/s2),
- a Foucault–féle inga kísérlet,
- az északi féltekén a lövedék jobbra térül el abból a síkból, amelyet kilövéskor a sebesség vektora meghatároz,

 

Hullám függvény, terjedési sebesség kötélhullám, hanghullám,

 

Def.: A hullámmozgás a rugalmas, deformálható test egy speciális mozgásformája. A deformálható testet úgy modellezzük, mint rezgő tömegpontok rendszere. Köztük a csatolás miatt halad tovább a harmonikus rezgésállapot. Ezt a zavart írja le a hullámfüggvény, ennek dinamikai számítását lehet a hullámegyenlettel elvégezni.

 

A hullámegyenlet, a hullámfüggvény

Tétel: A dinamika alapegyenletéből előbb származtatható a homogén, izotróp, rugalmas szilárd test általános, deformációs mozgását leíró, anyagállandókat tartalmazó differenciálegyenlet, abból pedig felírható a hullámegyenlet (ez annak az egydimenziós alakja):

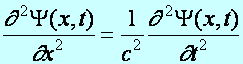       (d5.12)

 

ahol a Y(x,t) hullámfüggvény, az egy dimenzióban terjedő hullámot írja le, a c együttható pedig (amely általában a közeg anyagállandóiból íródik fel), a hullám adott közegbeli terjedési sebessége.

A síkhullámot leíró függvény két alakja:

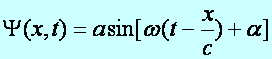  (d5.13)

felhasználva   (8.13) és 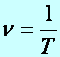           (d5.14)

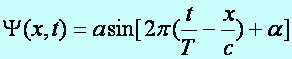       (d5.15)

 

Terjedési sebesség

A szilárd, rugalmas közegekben terjedő longitudinális (cl) és transzverzális (ctr) hullámok terjedési sebességét megadó kifejezésekben szerepelnek a közeg rugalmasságtani és egyéb anyagállandói (E, s, r):

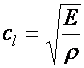
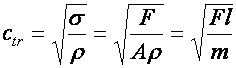           (d5.16)

 

A folyadékban terjedő longitudinális hullám terjedési sebessége a térfogati összenyomást jellemző anyagállandóktól (K, k), a sűrűségtől (r) és a nyomástól (p) függ. Ezt a hullámot levegőben és vízben hangnak nevezzük.
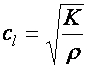
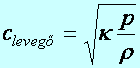          ahol k=1,41 (d5.17)

 

 

Laboratóriumi mérési gyakorlatok

 

D5 MECHANIKAI HULLÁMOK TERJEDÉSE RUGALMAS, DEFORMÁLHATÓ TESTEK BELSEJÉBEN ÉS FELÜLETÉN, HULLÁM TERJEDÉSI SEBESSÉGÉNEK MÉRÉSE. REZGÉSTAN, HULLÁMTAN

 

D5.1. Transzverzális hullám terjedése húron (gumicsövön). Terjedési sebesség mérése impulzus módszerrel.

D5.2. Transzverzális hullám terjedése húron (gumicsövön). Terjedési sebesség mérése rezonancia útján keltett állóhullámok vizsgálata alapján.

D5.3. Longitudinális hullám terjedése gázokban. Terjedési sebesség mérése rezonancia útján keltett állóhullámok vizsgálata alapján.

D5.4. Csatolt rezgések tanulmányozása kettős síkinga gyenge csatolású kis rezgéseinél.

D5.5. Alapvető hullámtani kísérletek hullámtállal.

D5.6 Két pontszerű forrásból kiinduló koherens hullám interferenciájának tanulmányozása hullámtállal.