Surlódásmentes folyadékok mennyiségei: sűrűség, nyomás és osztályozásuk

Def.: A folyadék olyan deformálható test, amelynek mind a térfogata, mind az alakja, vagy mindkettő könnyen megváltoztatható. Dinamikai szempontból a folyadék belsejében, mozgás során tapasztalt hatások szempontjából két csoportot különböztetünk meg: az ideális és a súrlódó folyadékot.

Def.: Ideális folyadék az olyan deformálható test, amelynél még mozgás közben sem lépnek fel érintőleges feszültségek (G=0).

Def.: Súrlódó (viszkózus) folyadék, amelynél mozgás közben a deformációs sebességekkel arányos, érintőleges feszültségek lépnek fel.

A folyadék mechanikában a tömeg fogalom szerepét a sűrűség veszi át, míg az erő fogalom szerepét pedig a nyomás.

Def.: (Mechanikai) sűrűség (jele: r) a test tömegének (m) és a test térfogatának (V) hányadosával definiált fizikai mennyiség. (Egysége: kg/m3):

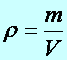(d4.1)

Def.: Nyomás (jele: p, pressure) az erő (F) és a felület (A) hányadosával definiált fizikai mennyiség, a folyadék normális feszültségeivel ellentétes hatás (a tekintetbe vett térfogat elem belső normálisa irányába számítjuk pozitívnak) (Egysége a feszültség egységével egyezik meg, tehát: N/m2):

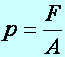(d4.2)

Az ideális folyadékok osztályozása során, aszerint, hogy a folyadék megtartja-e térfogatát, két csoportot különböztetünk meg.

Def.: Folyékony halmazállapotú testek (mint a víz, olaj, stb.), amelyek erőtérben nem tölti ki a rendelkezésükre álló teret, („összegyűlnek az edény alján”),

Def.: Légnemű halmazállapotú testek (pl. a levegő, ), amelyek kitölti a rendelkezésére álló teret, erőtérben pedig „felfelé” csökkenő sűrűséget mutatnak.

Az ideális folyadékok osztályozása során, aszerint, hogy a folyadék sűrűsége függ-e a rá nehezedő nyomástól, szintén két csoportot különböztetünk meg:

Def.: Összenyomhatatlan (inkompresszibilis) folyadék az olyan folyadék, amelynek a sűrűsége nem függ sem a helytől, sem az időtől (r=konst.).

Def.: Összenyomható (kompresszibilis) folyadék az olyan folyadék, amelynek a sűrűsége valamilyen függvénye a nyomásnak (r=konst.).

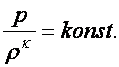
(d4.3)

fel a lap tetejére

Az ideális folyadék sztatikája Hidrosztatikai nyomás. Archimedes-féle törvény. Levegő sűrűségeloszlása. Sűrűség mérő módszerek

Tétel: (Nyugvó folyadék anyagegyenlete) A nyugvó folyadékot csak egy anyagegyenlet és ezzel egy anyagállandó a K kompresszió modulus jellemzi. Az anyagegyenlet megadja a nyomásnövekedés (Dp) okozta relatív térfogatcsökkenést (DV/V).

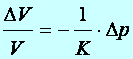(d4.4)

Tétel: (Pascal–tétel) Tömegerők hiányában, nyugvó, összenyomhatatlan folyadékban a nyomás bármely pontban független az iránytól (a nyomás izotróp).

A folyadékok "alakjával" kapcsolatban elsősorban a Föld felszínén vannak tapasztalataink. Egy edény, egy gödör, egy meder alja "telik" meg, pl. vízzel, egy pohár alja itallal és ekkor a folyékony anyag egy része érintkezik az "edény" falával, annak alakját ott ez szabja meg, de marad még a szabad felszíne és kérdés, milyen az. Milyen felülettel írható le a pohár vizének, a Balaton vizének, de a pohárban megkavart és ezért forgó teának a felszíne.

Ilyen esetek elemzése alapján azt a megállapítást tehetjük, hogy ebben a térfogati (v. tömeg) erőknek van szerepük. További kérdés, hogy milyen és mekkora hatást gyakorol ekkor a folyadék az edény fenekére, és a belemerülő más testre. Mindezeket három fontos tétel foglalja össze: A folyadékok egyensúlyának tétele, a hidrosztatikai nyomás összefüggése és az Archimedes–féle törvény.

Tétel: (Folyadékok egyensúlyának tétele) Ha a térfogati (v. tömeg) erők konzervatívak és a sűrűség csak a nyomás függvénye, a folyadékok egyensúlyban vannak, szabad felszínük minden része merőleges az ott uralkodó erőtér irányára.

Tétel: (Hidrosztatikai nyomás, Torricelli) A nehézségi erő (térerőssége = g) hatása alatt álló, összenyomhatatlan (r=konst.) folyadékban, a felszíntől mérve a nyomás (p) a mélységgel (z) lineárisan növekszik:

(d4.5)

Tétel: (Archimédesz–féle tőrvény ha a térfogati erő csak a nehézségi erő) Minden folyadékban (gázban) levő (szilárd) testre, ha a folyadék (gáz) a nehézségi erő hatása alatt áll, felhajtó erő hat (),

- melynek iránya felfelé mutat,

- nagysága megegyezik a test által kiszorított folyadék mennyiség súlyával (a folyadék sűrűsége, ρ, a test bemerülő részének térfogata Vtest),

-támadáspontja pedig a kiszorított folyadék mennyiség súlypontja:

(d4.6)

Megjegyzések: A "felhajtó erők" konkrét gyorsuló koordináta rendszerekben:

- egyenes mentén gyorsuló (transzlációs tehetetlenségi) rendszer:

(d4.7)

- egyenletesen forgó (centrifugális tehetetlenségi) rendszer:

(d4.8)

Tétel: (Barometrikus magasságformula) A nehézségi erőtérben (Föld felszíne közelében) levő gázban (izotermikus esetben) a nyomáseloszlást és a sűrűségeloszlást a következő összefüggések írják le (Levegő sűrűségeloszlása):

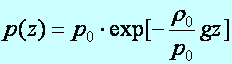(d4.9)

Ebben a po és a r a tengerszinten mért nyomás és sűrűség (levegő esetében 1033 hPa és 1,293 kg/m3). Tengerszinten ennek lineáris közelítése: 1 Hgmm nyomáscsökkenés 10,5 méterenként következik be.

A légnyomás mérésére, elsődlegesen a Torricelli–féle higanyos nyomásmérőt lehet használni. (Ez a levegővel alkot "közlekedő edényt".) Ezzel lehet hitelesíteni egyéb elveken működő nyomásmérő eszközöket. Vérnyomás meghatározására szintén használunk higanyos nyomásmérőt.

Sűrűség mérő módszerek, laboratóriumi gyakorlatok:

1. Folyadékok sűrűségének összehasonlítása közlekedő edényekben:

(d4.10)

2. Szilárd testek sűrűségének (ρ) viszonyítása az etalon folyadék sűrűségére (ρo):

(d4.11)

3. Keverék oldat eredő sűrűsége {ρ(x)}. Összetétel vizsgálata a sűrűség, mint anyagállandó mérése útján.

ahol (d4.12)

4. Sűrűségmérés úszó sűrűségmérővel.

fel a lap tetejére

Az ideális folyadék áramlása. Bernoulli-féle egyenlet.

Tapasztalatok:

- a házak között erősebben fúj a szél, mint a nyílt téren,

- a vízcsapból kifolyó víz elvékonyodik,

- az erős szélben megemelkednek a tető cserepei, stb.

Az ideális folyadék dinamikája, áramlástana úgy "beszél" a valódi folyékony és légnemű halmazállapotú testek mozgásáról, hogy a bennük működő erőket figyelmen kívül hagyja. Ez a leírása csak akkor alkalmazható, amikor a belső súrlódás valóságos esetekben elhanyagolhatóan kicsi.

Réteges áramlás. Bernoulli-féle egyenlet.

Def.: Réteges (lamináris) áramlás az olyan, amikor az áramló folyadék egymással párhuzamos vékony rétegekre osztható, amelyek egymás mellet különböző sebességgel mozognak.

Def.: Az áramerősség (jele: I', egysége: kg/s) a mechanikában leszármaztatott mennyiség, amelyet a tömeg és az idő hányadosaként ételmezünk. A technikában összenyomhatatlan folyadék (ρ) esetében a térfogat és az idő hányadosával van definiálva (jele: I, egysége: m3/s):

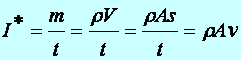(d4.13)

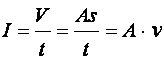
(d4.14)

Ideális folyadék áramlásának speciális esetei

időbeliség alapján:	időben állandó áramlás,
	időben változó áramlás,
folyadék részecskék végeznek–e	örvényes áramlás,
forgó mozgást, vagy sem:	örvénymentes áramlás
a sűrűség–nyomás függés alapján	összenyomhatatlan folyadék	r(p)=konst.
	összenyomható folyadék	r(p)≠konst.

Tétel: (Stacionárius áramlás változó keresztmetszetű fúvókákon = a kontinuitási egyenlet speciális esete) Változó keresztmetszetű vékony áramcsőben, összenyomhatatlan folyadék stacionárius áramlása esetén az áramerősség állandó:

(d4.15)

Tétel: (Bernoulli–féle egyenlet) Nehézségi erőtérben, súrlódásmentes, összenyomhatatlan folyadék, örvénymentes, stacionárius áramlása esetén a három nyomás dimenziójú tag összege az áramlási térben állandó:

(d4.16)

sztatikai	torló	hidrosztatikai nyomás
nyomás	nyomás

fel a lap tetejére

Súrlódó folyadék áramlása. Belső súrlódás. Hidrodinamikai ellenállás

Tapasztalatok:

- kanalat nehezebb a mézből kihúzni, mint a vízből,

- folyóban a víz sebesség középen nagyobb, mint a széleken,

- a szélben lobog a zászló,

- a repülőgép merev szárnyakkal repül,

- lehet egyre áramvonalasabb autót és repülőgépet csinálni, stb.

Megjegyzések: Az előző tapasztalatokkal kapcsolatban a következő dinamikai magyarázat tehető:

- különböző sebességgel mozgó szomszédos folyadék részecskék egymásra súrlódási erőt gyakorolnak,

- a mozgó folyadékban jelentkező feszültség tagoknak sebesség jellegű mennyiségeknek kell lenni, ez lesz a deformációs sebesség

Def.: Réteges (lamináris) áramlás az olyan, amikor az áramló folyadék egymással párhuzamos vékony rétegekre osztható, amelyek egymás mellet különböző sebességgel mozognak.

Newton a folyadékok belsejében mozgás közben ható erőhatást, a belső súrlódást erőtörvény formában írta le (ez a Newton–féle súrlódási törvény), és ebben a formában értelmezte a súrlódási állandót. A belső súrlódást csak réteges áramlásnál értelmezzük. Ennek megfogalmazása a következő:

Def.: Belsõ súrlódásról áramló folyadékoknál akkor beszélünk, amikor az A felülettel szemben, egymástól z távolságban levő, u sebességgel egymáson elcsúszó rétegek között ható F erő a következő összefüggés szerint számolható. (ez a felfogás egyébként Newton–féle súrlódási törvényként ismert):

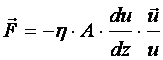(d4.17)

Ez összefüggés egyben a belső súrlódás jellemzésére alkalmazható anyagállandót, az h–t arányossági tényezőként tartalmazza.

Def.: A belső súrlódást (jele: h) csak réteges áramlásnál értelmezzük. Az h anyagállandó, amelynek a mértékegysége (N m-2 s), azaz Pa s (pascal secundum).

Tétel: Réteges áramlás csőben: (Hagen–Poiseuille–féle törvény, 1839) (Ohm–törvény alakban megfogalmazva) Összenyomhatatlan, súrlódó folyadék, stacionárius áramlásakor, kör keresztmetszetű csőben (sugara: R, hossza: l) az áramerősség (I=V/t) a nyomástól (p) a következő összefüggés szerint függ:

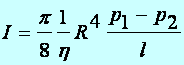
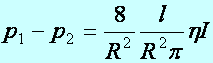U=R I (d4.18)

Megjegyzés: Ennek a törvényszerűségnek gyakorlati szerepe mind a vízvezetékek, mind pedig az erek mészkövesedése során bekövetkezett keresztmetszet változásában van.

Def.: Gomolygó (turbulens) áramlás az olyan, amikor

- az áramlás nem stacionárius, a sebesség és a nyomás egy meghatározott helyen nem állandó, hanem gyorsan ingadozik egy átlagérték körül,

- a folyadék részecskék pályái nemcsak, hogy nem egyenesek, nem is egyszerű görbék, hanem igen bonyolult módon egymásba fonódnak, a folyadék erősen összekeveredett,

- a cső végén az időegység alatt kiáramló folyadék térfogat sokkal kisebb, mint ami a p1-p2 nyomáskülönbség mellett a Hagen–Poiseuille törvény szerint adódna,

- a turbulens áramlásnál a cső "ellenállása" nagyobb, a folyadék viszkozitása látszólag megnövekedett.

Tétel: (Hidrodinamikai ellenállás) Ha egy összenyomhatatlan súrlódó folyadékban, amelynek r a sűrűsége, bármely A homlokfelületű test, olyan v sebességgel mozog, hogy a 103 < Re < 105 feltétel teljesül, a folyadék közegellenállását következő kifejezés adja meg:

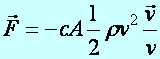(d4.19)

Tétel: (Reynolds–féle kifejezés, 1883) (jele: Re) A lamináris és a turbulens áramlások jellemzésére szolgáló egyik kifejezés a Reynolds–féle, amely a következőképpen írható fel:

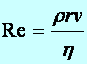(d4.20)

Megjegyzések: A Reynolds–féle kifejezés kritikus értéke, Rek=1160. Ha egy áramlás során Re<Rek, akkor az áramlás lamináris formája a stabilis, de ha Re>Rek, akkor pedig a turbulens forma a stabilis. Egy folyadék teljes ellenállását úgy értelmezzük, mint a súrlódási és az un. nyomási ellenállás összege.

Tétel: (Hidrodinamikai hasonlóság) Dinamikailag hasonló áramlásokhoz ugyanaz a Reynolds–féle szám tartozik:

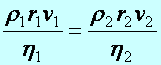(d4.21)

Megjegyzések: Létezik az un. Kármán–féle örvényút, ahol az örvények periódikusan és szimmetrikusan válnak le (Kármán Tódor, 1911). Prandtl–féle határréteg tétel: A folyadék viszkozitását csak a szilárd testet körülvevő vékony "határrétegben" kell tekintetbe venni, a szilárd testtől nagyobb távolságban a súrlódásmentes folyadékok hidrodinamikája alkalmazható.

fel a lap tetejére

Laboratóriumi mérési gyakorlatok.

D4. FOLYADÉKOK SZTATIKÁJA. ANYAGÁLLANDÓK MÉRÉSE

D4.1. Térfogati erő hatása alatt álló folyadék belsejében ható "felhajtó erő" vizsgálata. Folyadékok és szilárd testek sűrűségének relatív meghatározása Archimedes-féle mérlegelési módszerrel.

D4.2. Folyadékok és folyadék keverékek sűrűségének mérése relatív módon Mohr-Westphal mérleggel.

D4.3. Folyadékok felületi feszültségének tanulmányozása. Folyadékok felületi D4.feszültségének meghatározása abszolút, szakításos módszerrel.

D4.4. Folyadékok és folyadék keverékek felületi feszültségének relatív mérése sztalagmométerrel.

FOLYADÉKOK ÁRAMLÁSA. ANYAGÁLLANDÓK MÉRÉSE

D4.5. Áramló gázok sebességének mérése Pitot-féle, Pitot-Prandtl-féle és Ventúri-féle csövekkel a Bernoulli-féle egyenlet alkalmazásával.

D4.6. Folyadékok réteges és örvényes áramlásának tanulmányozása a Re=0-tól 10-ig terjedő intervallumon. A viszkozitás mérésének abszolút módja a Stokes-féle, valamint az Ossen-féle törvények alapján.

D4.7. Folyadékok réteges és örvényes áramlásának tanulmányozása a Re=0-tól 2000-ig terjedő intervallumon. A viszkozitás mérésének abszolút módja a Hage-Poiseuille-féle törvény alapján.

D4.8. Folyadékok és folyadék keverékek viszkozitásának relatív mérése az Ostwald-féle kapilláris viszkoziméterrel.

D4.9. Gázok örvényes áramlásának tanulmányozása a Re=5000-től 20000-ig terjedő intervallumon. Alaktényező meghatározása a hidrodinamikai ellenállás törvény alapján.

fel a lap tetejére