MECHANIKA - ELŐADÁS ANYAG
A merev test elemi mozgásformái: Transzláció, rotáció. Merev test szabadsági fokainak száma.
A merev testre ható erőrendszerek esetei
Forgatónyomaték. Erőpár. Merev test egyensúlya. Súlypont
Merev test forgása rögzített tengely körül, forgásegyenlet. Tehetetlenségi nyomaték.
Példák konkrét testek tehetetlenségi nyomatékára. Steiner-tétel
Merev test tengely körüli forgását vizsgáló és tehetetlenségi nyomatékot mérő gyakorlatok
Rugalmas szilárd test mechanikája. Feszültség, deformáció.
Elemi deformációk. Az elemi deformációkra vonatkozó erőtörvények. Anyagállandók
A rugalmas szilárd test anyagállandóit mérő (E és a G) gyakorlatok
Merev test mechanikája
Nagyon sok test mozgása során, a test lineáris méretéhez viszonyítva az alakváltozása nagyon kicsi, annak 1/100–ad, vagy 1/1000–ed része. Például: fém létra, amikor megyünk fel rá; Földünk az utóbbi 1–2 millió év alatt; szivacs, ha már eldobtam a levegőbe; sebesen forgó papírkorong, stb.
Az elhanyagolható módon deformálódó valóságos testek térbeli kiterjedését első közelítésben, a merev pontrendszerrel modellezhetjük. (Ezzel azonban elég "hézagosnak" képzeljük el a testet "cserében" matematikailag csak szorozni és összeadni kell). Ahhoz, hogy matematikailag eleget tegyünk annak a képnek, miszerint egy test folytonosan kitölti a rendelkezésére álló térrészt, a térfogati integrálást kell alkalmazni. Ezeknek megfelelően a matematikailag könnyebb és a nehezebb definíciók adhatók meg:
A merev test modell azzal több az egyetlen tömegpontra vonatkozó modellhez viszonyítva, hogy figyelembe veszi a valóságos testek térbeli kiterjedését. A belső kölcsönhatások külső hatásokra bekövetkező változását azonban nem képes leírni. Az elhanyagolható módon deformálódó valóságos testek térbeli kiterjedését első közelítésben, a merev pontrendszerrel modellezhetjük.
Def.: A merev test n számú diszkrét tömegpont merev rendszere, amit matematikailag meg lehet adni azzal, hogy az egyes tömegpontok távolsága állandó.
![]() i,j: 1,2,...,n
(d3.1)
i,j: 1,2,...,n
(d3.1)
A merev testnek a térbeli helyzetét, három, nem egy egyenesbe eső pontja már egyértelműen meghatározza. Ennek a három pontnak 3 x 3 = 9 koordinátája van. A merevség a három pont között, 3 egyenletet jelent. Így a merev test helyzetének megadásához 9 - 3 = 6 független adat elegendő. Így a merev test hat szabadsági fokú fizikai rendszer.
Def.: Szabadsági foknak nevezzük a mechanikában a rendszer független koordinátáinak a számát.
A hat független koordináta kiválasztásának az elve az, hogy meg legyen adva a test egy pontja egy "külső" koordináta rendszerben (K), valamint a testhez rögzített koordináta rendszer (K¢) tengelyeinek állása az előzőhöz képest. A kiválasztott pont lehet a test tömegközéppontja (ro, ez három adatot jelent), a K¢ origóját ebbe a pontba helyezhetjük, továbbá pedig megadhatjuk a K¢ tengelyeinek irányát, valamilyen megállapodás szerint a K tengelyeihez viszonyítva (ez szintén három adatot jelent). Később sorra kerülő számolások során belátható, hogy célszerű az un. Euler-szögekben megállapodni.
A merev test elemi mozgásformái: Transzláció, rotáció. Merev test szabadsági fokainak száma.
Def.: A merev test haladó mozgása (transzlációja) során egymással párhuzamos és egybevágó görbéket (speciálisan az egyenes vonalú transzlációnál egyenes szakaszokat) ír le, tehát a test térbeli irányultsága nem változik.
Def.: A merev test tengely körüli forgása, forgó mozgása (rotációja) során a test egy meghatározott egyenesen (a forgástengelyen) levő pontjai helyüket változatlanul megtartják, míg a test többi pontja a forgástengelyre merőleges síkokban köríveket ír le.
Tétel: A merev test bármilyen elmozdulása egy transzlációból és egy rotációból tehető össze.
Példák a merev test különböző szabadsági fokú mozgásformáira:
1. f = 6. Merev test térbeli szabad mozgása (Pl. toronyugró legnehezebb gyakorlatok során; autó kereke a Mecsek szerpentinjein kanyarogva).
2. f = 5. Síkban gördülő golyók (Pl. golyó a biliárd asztalon).
3. f = 4. Síkban gördülő, kanyarodó kerék (Pl. autó kormányzott kereke sík terepen).
4. f = 3. Egy pontjában rögzített test mozgása (Pl. "súlyos" pörgettyű, erőmentes pörgettyű). Merev test síkmozgása (Pl. légpárnás asztalon korongok mozgása).
5. f = 2. Merev test egy síkban történő haladása és forgása (Pl. henger, golyó legördülése lejtőn, autó kerék mozgása síkban, egyenes mentén).
6. f = 1. Merev test forgása rögzített tengely körül (Pl. egyhelyben levő motorok forgó alkatrészei).
7. f = 0. Merev test nyugalomban.
A merev testre ható erőrendszerek esetei:
A merev testre ható erő ismerete azt jelenti, hogy ismerjük a támadáspontját, a nagyságát, irányát (hatásvonalát). A merev testre ható erők támadáspontjuk, nagyságuk, irányul és hatásvonaluk alapján lehetnek különbözők. Megmutatható, hogy több erő hatása helyettesíthető–e egyetlen erővel, kivéve az erőpár esetét.
Tétel:
(Erőrendszer redukálása) A merev test A1,
A2, ,An,
pontjaiban támadó
![]() erők rendszere helyettesíthető egy, a test tetszőleges
O pontjában támadó
erők rendszere helyettesíthető egy, a test tetszőleges
O pontjában támadó
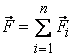 erővel és egy
erővel és egy
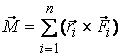 nyomatékú erőpárral, ahol
nyomatékú erőpárral, ahol
![]()
Megjegyzések: Az előzőekkel a merev test elemi mozgásformáinak (transzláció, rotáció) dinamikai feltételét le tudjuk írni. Azzal, hogy egy erőrendszer redukálása során az erők eredőjét tetszőleges pontban vehetjük fel, lehetőségünk van azt a test tömegközéppontjában támadónak felvenni, a "generált" erőnyomaték pedig egy, a tömegközépponton átmenő tengely körüli forgást eredményez.
Forgatónyomaték. Erőpár. Merev test egyensúlya. Súlypont.
Def.: Egy erő forgatónyomatéka (M) egy adott tengelyre vonatkoztatva az erő tengelyre merőleges síkra eső vetületének (F) és ezen vetület hatásvonalának a tengelytől mért távolságának (k) a szorzatával számolható (egysége: Nm)
![]() (d3.2)
(d3.2)
Def.: Az erőpár két különböző támadáspontú, párhuzamos hatásvonalú, ellentétes irányú és azonos nagyságú erő együttese.
Tétel: Az erőpár a legegyszerűbb olyan erőrendszer, amely nem helyettesíthető egyetlen erővel. Az erőpár nyomatéka a következőképpen számolható:
![]() (d3.3)
(d3.3)
Tétel: (Merev test egyensúlyának tétele) Egy merev test akkor van egyensúlyban, ha a rá ható erők eredője zérus és a rá ható erők (tetszőleges pontra vonatkoztatott) nyomatékainak eredője is zérus:
ha
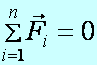 , és
, és
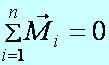 , akkor egyensúly
(d3.4.)
, akkor egyensúly
(d3.4.)
Def.: Egy merev test esetében azt a térbeli pontot tekintjük súlypontnak, amely pontra vonatkoztatva a merev test mindenegyes elemére ható súlyerő nyomatékának eredője zérus. Az előző tétel egy következménye a súlypont definíciója:
Tétel: Homogén erőtérben (pl. nehézségi erőtér) a súlypontba mutató helyvektor megegyezik a tömegközéppontba mutató helyvektorral (más szóval a súlypont a tömegközépponttal).
Megjegyzések: A súlypontban felfüggesztett (alátámasztott) test közömbös, a súlypont fölött felfüggesztett test stabilis, míg a súlypont alatt alátámasztott test labilis egyensúlyi helyzetben van.
A kétkarú mérleg (amely erő és tömeg mérésére létrehozott célkészülék) "működését" a merev test egyensúlya tétel alapján tárgyalhatjuk le.
Nem homogén erőtérre példa a gravitációs erőtér, a "centrifugális erőtér", a Coriolis–féle erőtér, amelyekben a súlypont nem meghatározott (függ a test helyzetétől), míg a tömegközéppont a testnek mindig azonos helyén van.
Merev test forgása rögzített tengely körül. Forgásegyenlet. Tehetetlenségi nyomaték.
Tétel: (Tengely körül forgó merev test mozgásegyenlete, forgásegyenlete) Egy z tengely körül forgó merev test forgásegyenlete a következő alakú (a tehetetlenségi nyomaték (Qz) és a szöggyorsulás (b) szorzata egyenlő a ható erők forgatónyomatékával, Mz–vel):
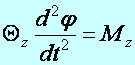 (d3.5)
(d3.5)
Def.: Az i–dik tömegpont (melynek tömege mi) z tengelyre vonatkoztatott tehetetlenségi nyomatékán (Qz,i), (ha a z tengelytől mért távolságát li–vel jelöljük), a következő szorzatot értjük:
![]() (d3.6)
(d3.6)
Def.: Az n számú tömegpontból álló merev test z tengelyre vonatkoztatott tehetetlenségi nyomatékán (Qz) az egyes tömegpontok z tengelyre vonatkoztatott tehetetlenségi nyomatékainak (skalár) összegét értjük:
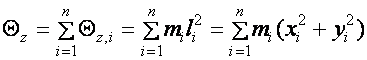 (d3.7)
(d3.7)
Tétel: (Tengely körül forgó merev test forgási energiája, Em,r) Egy z tengely körül forgó merev test forgási energiáját a tehetetlenségi nyomaték (Qz) és a szögsebesség (w) ismeretében a következő összefüggés alapján lehet kiszámolni:
![]() (d3.8)
(d3.8)
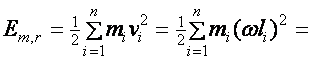
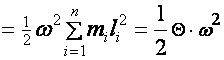 (d3.9)
(d3.9)
Példák konkrét testek tehetetlenségi nyomatékára, Steiner-tétel
A gyakorlatban csak homogén tömegeloszlású, szabályos alakú testek szimmetria tengelyeire (a szimmetria tengely átmegy a tömegközépponton) számolják ki integrálással közvetlenül a Q értékét. Néhány test tömegközéppontján átmenő tengelyre vonatkoztatott tehetetlenségi nyomatéka:
1. Rúd hosszára merőlege tengelyre
![]() (d3.10)
(d3.10)
2. Körlapra merőleges tengelyre
![]() (d3.11)
(d3.11)
3. Cső szimmetria tengelyére
![]() (d3.12)
(d3.12)
4. Gömb
![]() (d3.13)
(d3.13)
Ezen értékekből, párhuzamos tengelyek között a Steiner–tétel; a szöget bezáró tengelyek között a tehetetlenségi tenzor alkalmazásával lehet tovább számolni.
Tétel: (Steiner–tétel) Ha ismert egy m tömegű merev test tömegközéppontján (O) átmenő tengelyre vonatkoztatott tehetetlenségi nyomatéka (Qo), akkor ebből az adatból egy (tetszőleges (A) ponton átmenő) vele párhuzamos, s távolságra levő tengelyre vonatkoztatott tehetetlenségi nyomatékot (QA) a következő összefüggés alapján számolunk ki:
![]() (d3.14)
(d3.14)
Tétel: A tengely körül forgó merev test impulzus nyomatékát (N) a tehetetlenségi nyomaték és a szögsebesség szorzataként lehet kiszámolni:
![]() (d3.15)
(d3.15)
Laboratóriumi mérési gyakorlatok
D3. Testek tengely körüli forgását, rezgését vizsgáló és tehetetlenségi nyomatékot mérő gyakorlatok:
D3.1. Egyenletesen változó forgó mozgás függőleges tengely körül.
D3.2. Harmonikus forgó rezgést végző korong vizsgálata. Tehetetlenségi nyomaték mérése.
D3.3. Hengeres test legördülése lejtőn
D3.4. Fizikai inga lengése
D3.5. Fizikai inga rezgésének vizsgálata száraz csillapítás esetén.
D3.6. Fizikai inga rezgésének vizsgálata folyadék csillapítás esetén. Csillapítási tényező mérése.
Rugalmas szilárd test mechanikája. Feszültség, deformáció.
Tapasztalat: Nagyon sok test mozgása során, vagy adott helyen "nyugalomi állapotában" tapasztalható az, hogy mérete, alakja jelentősen változik. Például:
- a csavarrugó, a gumiszalag megnyúlik, ha súlyt akasztok rá,
- a szivacs összenyomódik, ha megszorítom,
- a hosszú deszka behajlik, ha a két végénél alátámasztom,
- a fa hajladozik, ha fújja a szél,
- a víz követi a vízvezeték hálózatot, a csapoknál kifolyik, majd szétfröcsög,
- a folyóban örvények keletkeznek a híd lábánál,
- a szappanbuborék, léggömb felfújódik, ha fújjuk,
- a vajjal megkenem a kenyeret, stb.
A szilárd rugalmas test modell azzal több a merev test modellhez viszonyítva, hogy nem csak a valóságos testek térbeli kiterjedését veszi figyelembe, hanem a belső kölcsönhatások külső hatásokra bekövetkező változását is igyekszik leírni.
A deformálható test modell esetében jellemző fogalom a halmazállapot. A deformálhatóság "mértékéül" a térfogattartást és az alaktartást alkalmazhatjuk. Ezek kombinációja alapján halmazállapotokat különböztetünk meg.
AlakTérfogat |
VAN |
NINCS |
VAN |
SZILÁRD |
FOLYÉKONY |
|
NINCS |
------- |
LÉGNEMŰ |
A deformálható testeknek más testekkel történő kölcsönhatásának figyelembe vételénél még inkább szükséges azok hatását a következő két csoportra osztani: térfogati erők (mechanikában tömegerők), felületi erők.
Def.:
Térfogati erő v. tömegerő az olyan erő (egy térerősséggel
arányos), amely a test minden részére, belső és felületi részére egyaránt
hat, tehát a
DV
térfogatelemmel, vagy a
Dm
tömegelemmel arányos. Jele:
![]() .
.
![]() (d3.16)
(d3.16)
Def.:
Felületi erő az olyan erő, amely a
DV
térfogatelemre csak az ezt körülhatároló
Df
felületelem közvetítésével hat. Ez az erő a
Df–fel
közvetlenül szomszédos külső részektől származik és a
Df–fel
arányos. Jele:
![]() . A felületi erő kifejezhető úgy, mint a feszültség
vektorral (Jele:
. A felületi erő kifejezhető úgy, mint a feszültség
vektorral (Jele:
![]() , egysége: N/m2)
arányos mennyiség:
, egysége: N/m2)
arányos mennyiség:
![]() (d3.17)
(d3.17)
Def.: Az ideális szilárd test olyan, amelyben mind dilatáció (nyújtás), mind pedig torzió (nyírás) előidézhető, amely deformációk során keletkeznek, mind húzó, mind pedig nyíró feszültségek. Mind a 6 db anyagállandó zérustól különböző.
Def.: Az ideális folyadék olyan test, amelyben kompresszió következtében, nyugalmi állapotban (ill. kvázi nyugalmi állapotban = lassú deformációk során) csak normális (húzó, nyomó) feszültségek keletkeznek, tangenciális (érintőleges) feszültségek nem lépnek fel. Csak 3 db anyagállandó nem zérus.
Elemi deformációk. Az elemi deformációkra vonatkozó erőtörvények. Anyagállandók
Az ideális (tökéletesen rugalmas, homogén, izotróp) szilárd test mozgásegyenlete 2 db anyagállandót tartalmaz. Ezért a konkrét anyagok (pl. vas, réz, stb.) rugalmasságtani tárgyalásához szükség van két "kívülről" bevitt adatra (ezek anyagállandóira), amelyeket kísérletileg kell meghatározni. Ez az un. anyagállandókkal dolgozó fenomenológiai tárgyalás. Jelen esetben csak az egyensúly tárgyalására kerül sor
A rugalmas szilárd testre, ha külső felületi erő hat, az ennek következtében deformálódik. A létrejött deformáció során "ébredt" feszültségek kiegyenlítik a külső erők hatását, beáll az egyensúly.
Elemi deformációk: osztályozás a test két, egymással párhuzamos lapjának térbeli összes lehetséges elmozdulása alapján történik.
1. Nyújtás, harántösszehúzódás: Ekkor a szemközti párhuzamos lapok síkjukra merőleges irányban mozdulnak el.
 (d3.18)
(d3.18)
A rúd hossza l, keresztmetszete A, megnyúlása Dl. F nagyságú a húzóerő. Az E betűvel jelölt mennyiséget rugalmassági, vagy Young–féle modulusnak nevezzük. Értéke vas esetében 21x1010 N/m2.
2. Minden oldalú összenyomás: Ekkor minden szemközti oldal egymás felé mozdul el.
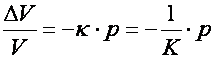 (d3.19)
(d3.19)
A V térfogatú test felületét mindenütt ugyanakkora, merőlegesen befelé mutató nyomás (p) éri. A térfogatváltozás DV. A k betűvel jelölt mennyiséget kompresszibilitásnak, a K betűvel jelölt mennyiséget pedig térfogati rugalmassági tényezőnek, kompressziómodulusnak nevezzük. A K mértékegysége: N/m2.
3. Hajlítás: Ekkor a szemközti párhuzamos lapok által bezárt szög változik.
4. Nyírás (csúsztatás): Ekkor a szemközti párhuzamos lapok eredeti térbeli irányukhoz képest elfordulnak.
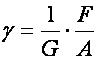 (d3.20)
(d3.20)
Egy A alapú hasábra, F nagyságú erő hat a felső lap síkjában. Ekkor azok az élek, amelyek az erőre merőlegesek voltak, elfordulnak, ez a szög g. A G betűvel jelölt mennyiséget nyírási, csúsztatási, vagy torzió modulusnak nevezzük. Értéke vas esetében 7x1010 N/m2.
5. Csavarás: Ekkor a szemközti párhuzamos lapok párhuzamosak maradnak, csak egyik a másikhoz képest elfordul.
A rugalmas szilárd test anyagállandóit mérő (E és a G) gyakorlatok:
1 Az E sztatikus úton történő meghatározása hosszirányú feszítő erővel. Az E sztatikus úton történő meghatározása huzalra merőleges feszítő erővel. Az E sztatikus úton történő meghatározása laprugóra merőleges erővel.
2 A G sztatikus úton történő meghatározása elcsavarással.
3 Az E dinamikus úton történő meghatározása laprugó rezgésének vizsgálata útján.
4 A G dinamikus úton történő meghatározása huzal torziós rezgéseinek vizsgálata útján.