MECHANIKA - ELŐADÁS ANYAG
Newtoni dinamika kiépítéséhez vezető alapelvek.
A Newton-féle axiómák. Tömeg, erő.
A dinamika alapegyenlete.
A dinamika alapegyenletének
"alkalmazási területei": Erőtörvények Mozgás tárgyalása. Tehetetlen
tömeg mérése.
Mechanikai feladat
megoldásának elvi kérdései a dinamika alapegyenlet alapján
Munka, munkatétel, mozgási energia
Konzervatív erő. Helyzeti energia formák
Pontrendszer mechanikája. Külső, belső erők. Impulzus. Impulzustétel. Impulzus megmaradás tétele.
A mechanika megmaradási tételei
Mechanikai feladat megoldásának
elvi kérdései az anyagi pont mechanikájának teljes ismeretében
Newtoni dinamika kiépítéséhez vezető alapelvek.
Az AP legegyszerűbb mozgásait abból a szempontból, hogy előfordul-e gyorsulás vagy sem, két csoportba oszthatjuk. Az első csoportba csak az egyenes vonalú egyenletes mozgás tartozik, a második csoportba pedig az összes többi.
A mozgó testek megfigyeléséből azt a következtetés sorozatot vonhatjuk le, hogy egy test egyre kevésbé tér el egyenes vonalú mozgásától, továbbá egyre kevésbé változik a sebességének nagysága (vektori alakban megfogalmazva egyre kevésbé változik a sebességét jellemző vektor), ha egyre inkább sikerül biztosítani, hogy a vizsgált testre ható más testek kikompenzálják egymás hatását. Ha a vizsgált test mozgásállapot változásáért (gyorsulásáért) egy másik test hatását „okoljuk”, akkor ez a „hozzáállás” a jelenség leírásához, a Newtoni-mechanika.
A Newtoni-mechanika alapvető elvei, fundamentális gondolatai a következők:
- feltételezzük, hogy a testek hatnak egymásra (kölcsönhatásban vannak, egyik hat a másikra; a másik hat az elsőre; egyik erő, másik erő),
- a kölcsönhatásban az egyik test hatását a másikra, tesszük "felelőssé" a másik mozgásállapotának változásáért, és feltételezzük, hogy ez jellemezhető majd fizikai mennyiséggel, amely "első körben" csak a test helyétől, sebességétől és az időtől függ (newtoni erő),
- több test egyidejű hatása esetében feltételezzük azok függetlenségét,
- feltételezzük, hogy a mozgásállapot megváltozásban "résztvevő" test jellemzésére is bevezethetünk egy fizikai mennyiséget a tehetetlen tömeget,
- végül pedig az egyik test hatása (az erő), a másik test tehetetlenségének mértéke (a tömeg) és a mozgásállapot megváltozását jellemző kinematikai mennyiség (gyorsulás) között feltesszük, hogy felírható egy vektoriális alakban megadott összefüggés (alapvető, egyenletben megfogalmazott állítás),
- majd általánosítjuk az erő fogalmat úgy, hogy nemcsak akkor beszélünk róla, amikor kölcsönhatást észlelünk, hanem akkor is, amikor egy testnek csak a mozgásállapot változását tapasztaljuk (nem–newtoni erő).
Megjegyzés: A legáltalánosabbnak tekintett megállapításokat Newton axiómáknak nevezzük (máshol Newton-féle alaptörvényeknek, röviden Newton-törvényeknek nevezik őket). A megfogalmazásokban a matematikából kulcsszerepet játszik az algebra, a geometria (vektorok) és a differenciál-integrál számítás (időbeli változás, összegzés leírása). Ezek alkalmazásával érhető el, hogy a leírás kvantitatív legyen (tehát számolni lehessen velük). Ez a leírás erő-tömeg-gyorsulás koncepciójú. Nem használja az alapvető állításában a test lendületét (impulzusát). (nem lendületváltozás-erő koncepciójú, mint Newton eredeti megfogalmazásában). Még inkább nem energia koncepciójú leírás (nem Hamilton-, vagy Lagrange-féle mechanika.
A Newton-féle axiómák. Tömeg, erő.
I. axióma: (Tehetetlenség törvénye) Található olyan vonatkoztatási rendszer, amelyben minden test megtartja egyenes vonalú egyenletes mozgásállapotát mindaddig, amíg rá más test nem hat.
II. axióma:
(Erő, tömeg, gyorsulás kapcsolata)
Egy test (A) gyorsulása (![]() ),
),
- egyenesen arányos a rá ható másik test (B) hatásával (![]() ), és
), és
- fordítottan arányos a saját tehetetlenségének mértékével, a tömegével
(mA),
- gyorsulása az erő irányába következik be (![]() ||
||![]() )
)
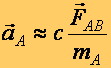 (d2.1)
(d2.1)
A II axióma, ha a lehetséges arányossági tényezőt, (c) egységnyinek és nulldimenziójúnak választjuk, a következő alakban írható fel:
![]() tömören
tömören
![]() (d2.2)
(d2.2)
Ebben az egyenletben csak a gyorsulás fizikai mennyiség, az erő és a tömeg fizikai mennyiségként történő értelmezésére most van lehetőség. Egy egyenletből csak egy mennyiséget lehet leszármaztatni, a mási kettőnek már értelmezettnek kell lenni. A fizika úgy „döntött”, hogy újabb alapmennyiségnek a tömeget vezeti be, ekkor az erő már leszármaztatott mennyiség lesz.
Def.: A (tehetetlen) tömeg (massa, jele: mt, röviden m) a testnek gyorsuló mozgása során a gyorsítással szemben mutatott tehetetlenségének a mértéke, ennek jellemzésére bevezetett alapmennyiség.
Def.: 1 kilogramm (röviden kg) annak a testnek a tömege, amelyet a Francia Mérésügyi Hivatalban őriznek.
Def.:
Egy testnek (pl. B-nek) egy másik testre (pl. A-ra) gyakorolt hatását
röviden erőnek (dinamos, force, jele:
![]() , röviden
, röviden
![]() ) nevezzük. Az erőt irányított mennyiségnek
fogjuk fel.
) nevezzük. Az erőt irányított mennyiségnek
fogjuk fel.
Def.:
1 Newton annak az erőnek a nagysága, amely (pl.) az egy kilogramm
tömegű testet egy
![]() gyorsulással mozgatja.
gyorsulással mozgatja.
Def.:
Az m tömegű és
![]() sebességű anyagi pont impulzusa (lendülete,
jele:
sebességű anyagi pont impulzusa (lendülete,
jele:
![]() , vagy
, vagy
![]() ) a tömeg és a sebesség szorzatával definiált fizikai
mennyiség, azaz
) a tömeg és a sebesség szorzatával definiált fizikai
mennyiség, azaz
![]() . Egysége: 1 kg m s-1.
. Egysége: 1 kg m s-1.
II. axióma:
(Impulzussal megfogalmazva) A
tömegpont impulzusának idő szerinti első differenciálhányadosa egyenlő a
TP–ra ható erővel:
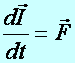 (d2.3)
(d2.3)
III. axióma:
(Hatás–ellenhatás törvénye) Ha egy pontszerű A testre a pontszerű
B test erőt (![]() ) gyakorol, akkor az A test is hat B-re (
) gyakorol, akkor az A test is hat B-re (![]() ), ugyanolyan nagyságú és ellentétes irányú erővel:
), ugyanolyan nagyságú és ellentétes irányú erővel:
![]() (d2.4)
(d2.4)
Megjegyzések:
IV axiómaként is szokták említeni azt, hogy
az erőket vektorként fogjuk fel, és összegüket a vektori összeadás
szabályai szerint számoljuk ki. Ez azt is jelenti, hogy az erők
független szuperpozicióját tételezzük fel.
![]() tömören
tömören
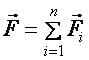 (d2.5).
(d2.5).
A dinamika alapegyenlete. "Alkalmazási területei": Erőtörvények. Mozgás tárgyalása. Tehetetlen tömeg mérése.
Tétel: Dinamika alapegyenletének nevezzük azt a másodrendű vektori differenciálegyenletet, amelyet a IV. axiómával kiegészített II. axióma formájában írunk fel úgy, hogy a gyorsulást a helyvektor időszerinti második differenciálhányadosaként értelmezzük:
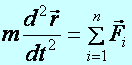 egyszerűen
egyszerűen
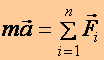 (d2.6)
(d2.6)
komponens egyenletei:
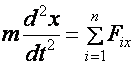
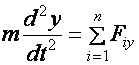
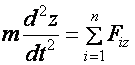 (d2.7)
(d2.7)
Megjegyzések: A fenti, vektori alakban felírt differenciálegyenlet egy tömörített írásmód, számolásra a három komponens egyenlet szolgál. Ezen egyenletek megoldása azt jelenti, hogy megkapjuk adott erő(k) hatására a térbeli pálya komponenseinek időfüggvényét.
A dinamika
alapegyenletének "alkalmazási" területei:
1. Erőtörvények "megsejtése".
2. Mozgásegyenletek felírása, megoldása.
3. Tehetetlen tömeg mérése, dinamométer hitelesítése
Erőtörvények "megsejtése". Ez úgy történik, hogy a megfigyelések, kísérletek során meghatározzák a mozgó test gyorsulását, a kapott értéket beírják a dinamika alapegyenletébe, amely alapján kapnak egy kifejezést az erőre:
- nehézségi erő
erőtörvénye: a Föld gravitációs hatásának konstans közelítése a Föld
felszínén
![]() (d2.8)
(d2.8)
- gravitációs erő erőtörvénye: az
egyik anyagi pont (1-es) hatása a másikra (2-esre)
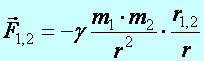 ahol
ahol
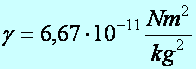 (d2.9)
(d2.9)
- rugalmas típusú erő erőtörvénye:
az erő a kitéréssel ellentétes és azzal arányos
![]() (d2.10)
(d2.10)
- Coulomb-féle
csúszási súrlódási erő: amely a nyomóerővel arányos és ellentétes a
mozgás irányával
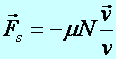 (d2.11)
(d2.11)
2. Mozgásegyenletek felírása, megoldása. Ennek során az erők matematikai alakját feltételezve, fel kell írni a differenciál egyenletet, amelynek megoldása a feltételezett erő hatása alatt álló TP pályafüggvénye. A differenciál egyenlet még egyszerűen megoldható pl. a lineáris erőtörvény (F=–Dx) esetén. Ekkor a megoldandó differenciálegyenlet alakja és megoldásfüggvénye a következő:
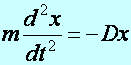 (d2.12)
(d2.12)
![]() (d2.13)
(d2.13)
3. Tehetetlen tömeg mérése tömegetalon felhasználásával, gyorsulás mérésével. Erre minden olyan mozgásforma alkalmazható, ahol gyorsul a test. A mérés során az etalon tömegű testnek és az ismeretlen tömegű testnek a gyorsulását kell megmérni, és megfelelő számítások alapján a vizsgált test tömegét megkapjuk. Példa erre a rugóra akasztott test rezgése (tömegmérés „súlytalanság” esetében).
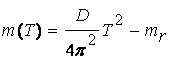 (d2.14)
(d2.14)
Feladat megoldás elvi kérdései a dinamika alapegyenlet alapján:
Erőtörvényekkel megadott erőkkel felírt
dinamika alapegyenletből számolhatók:
- kinematikai mennyiségek (![]() ,
,
![]() ,
,
![]() ),
),
- kényszererők (fonalerő, nyomóerő).
Mechanikai feladat megoldásának lépései a dinamika alapegyenlet alapján:
1) Kiírom a feladat megadott mennyiségeinek adatait (SI).
2) A test teljes mozgását annyi szakaszra bontom térben és időben, hogy egy–egy szakaszon a mozgás elemi mozgásformák valamelyikével közelíthető legyen.
3) Döntök arról, hogy milyen erőket (mely testek hatását) veszek figyelembe a vizsgált test mozgásának tárgyalásához.
4) Optimális módon "felveszem" a koordináta rendszert. Ezen jelölöm a mozgást és a mennyiségeket.
5) Felírom a vektor mennyiségeket
(![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,..)
koordinátáikban.
,..)
koordinátáikban.
6) Felírom koordinátákkal a dinamika alapegyenletének komponens egyenleteit.
7) Felírom a feladat teljes kinematikai leírását.
8) Felírom a feladatban megadott kényszer- és határfeltételeket egyenletek formájában.
9) Megállapítom, hogy a feladat matematikailag egyértelműen megoldható–e, vagy sem (Egyenletek száma, ismeretlenek száma).
10) Programot készítek arról, hogy milyen sorrendben számolom ki az ismeretleneket. Diszkutálom a kapott eredményeket. (Van-e hamis eredmény?)
Munka, munkatétel, mozgási energia
Megjegyzések:
A tömegpont mozgásának leírása a dinamika alapegyenletével tökéletesen
megtörténhet. Ezen gondolkodásmód szerint akkor mondom, hogy "ismerem a
tömegpont mozgását" (azaz le tudom írni azt), ha
- meg tudom nevezni az erőket (fel tudom írni az erőtörvényüket),
- meg tudok adni egy koordináta rendszerben kezdőfeltételeket (t=0
időpontban hol volt, milyen irányban és milyen sebességgel haladt),
- meg tudom oldani a dinamika alapegyenletét az előző adatokkal (azaz
tudok egyértelműen megoldásfüggvényeket találni a differenciál
egyenletek tárgykörében, vagy tudok elfogadható közelítéseket tenni úgy,
hogy megoldható egyenletre jussak),
- "melléktermékként" megkapom a kényszererők értékét is.
A tömegpont mozgásának leírása a dinamika alapegyenletével tökéletesen megtörténhet. A nehézségi erő (G=mg, integrálható egyenlet) és a rugóerő (F=-Dx, harmonikus rezgőmozgás differenciálegyenlete) erőtörvények esetében egyszerű számítások, meggondolások alapján egzakt megoldást kapunk. A matematikai inga tárgyalása során azonban már közelítéssel élünk.
Nagyon gyakran, még napjainkban is (amikor numerikus módszerek és nagy sebességű számítógépek állnak rendelkezésre) a matematikai nehézségek komoly akadályt jelentenek az összetettebb problémák dinamika alapegyenlete szerinti megoldásánál.
Ebből a helyzetből az anyagi pont mechanikáján belül is lehet tovább lépni. Ezt tesszük most új fogalmak és egyszerűbb matematikai tárgyalásmód bevezetésével. Lehet egyébként más koncepciójú mechanikát is kiépíteni (pl. Lagrange–féle mechanika, Hamilton–féle mechanika).
A munka fogalmának kialakítása a fizikában
Célszerű a mechanikában is definiálni egy olyan mennyiséget, mint amit a hétköznapi életben munka szóval illetünk. Az ember olyankor, amikor fizikai munkát végez, úgy fogalmaz, hogy erőt fejt ki, amely hatására valami (egy test) térben elmozdul, ezzel az ember erejének "támadáspontja" is elmozdul. Ebből az "élményből fakad" a mechanikában bevezetésre kerülő munka fogalmának is a definíciója.
Def.: A munka (work, jele: W) az erő (F) és a hosszúság (l) szorzataként értelmezett fizikai mennyiség. A munkát skalár mennyiségként fogjuk fel. Egysége: kg m2 s-2 = N m = J (Joule).
![]() (d2.19)
(d2.19)
A munkának számolásra alkalmas két definícióját emeljük ki. Az egyik matematikai szempontból elemibb, a másik pedig az általánosabb forma:
Def.:
Egy
![]() (állandó) erő munkáját (W), amikor annak
támadáspontjának elmozdulása egy egyenes mentén
(állandó) erő munkáját (W), amikor annak
támadáspontjának elmozdulása egy egyenes mentén
![]() , az erő és az elmozdulás vektorok skaláris
szorzatával lehet kiszámítani:
, az erő és az elmozdulás vektorok skaláris
szorzatával lehet kiszámítani:
![]() (d2.20)
(d2.20)
Def.:
A hely szerint változó erő (![]() ) munkáját, miközben annak támadáspontja az
) munkáját, miközben annak támadáspontja az
![]() helykoordinátával jellemzett helyről az x
tengely mentén az
helykoordinátával jellemzett helyről az x
tengely mentén az
![]() helyvektorral jellemzett helyre jutott el, az erő
helyvektorral jellemzett helyre jutott el, az erő
![]() ,
,
![]() pontok közötti határozott integráljával lehet
kiszámítani:
pontok közötti határozott integráljával lehet
kiszámítani:
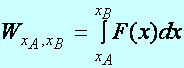 (d2.21)
(d2.21)
Példák a mechanikai erők munkájának számítására
a.
A nehézségi erő (![]() = -mg) munkája (
= -mg) munkája (![]() ) a felfelé (zA=0,
zB=h) repülő
m tömegű tömegpont esetében a következőképpen számolható:
) a felfelé (zA=0,
zB=h) repülő
m tömegű tömegpont esetében a következőképpen számolható:
![]() (d2.22)
(d2.22)
b.
A rugalmas erő (![]() ) munkája (
) munkája (![]() ), miközben az m tömegű TP az egyensúlyi
helyzettől (xA=0)
távolodik (xB=xo),
a következőképpen számolható:
), miközben az m tömegű TP az egyensúlyi
helyzettől (xA=0)
távolodik (xB=xo),
a következőképpen számolható:
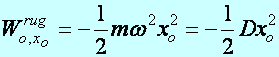 (d2.23)
(d2.23)
c.
Az m1 tömegű
tömegpont gravitációs erejének (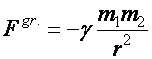 ) munkája (
) munkája (![]() )
miközben az m2 tömegű
TP az ro távolságból
a végtelenbe (
)
miközben az m2 tömegű
TP az ro távolságból
a végtelenbe (![]() ) repül, a következőképpen számolható:
) repül, a következőképpen számolható:
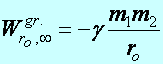 (d2.24)
(d2.24)
Munkatétel
Tétel:
(Munkatétel, MT) A tömegpont mozgási energiájának megváltozása (a
későbbi időpontbeli, t2,
és a korábbi időpontbeli, t1 mozgási
energia különbsége) egyenlő a tömegpontra ható erők eredőjének
munkájával,
![]() (miközben az erők támadáspontja az adott pályán a t1 időpontban
levő helyről elmozdul a t2 időpontbeli
helyre):
(miközben az erők támadáspontja az adott pályán a t1 időpontban
levő helyről elmozdul a t2 időpontbeli
helyre):
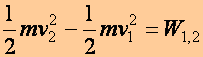 (d2.25)
(d2.25)
Def.:
Az m tömegű és
![]() sebességű TP mozgási (kinetikai) energiájának
(kinetic energy, jele: Em,
vagy Ek)
nevezzük a következő szorzattal megadott fizikai mennyiséget (Egysége:
kg m2 s-2 =
N m = J (Joule)):
sebességű TP mozgási (kinetikai) energiájának
(kinetic energy, jele: Em,
vagy Ek)
nevezzük a következő szorzattal megadott fizikai mennyiséget (Egysége:
kg m2 s-2 =
N m = J (Joule)):
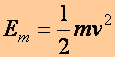 (d2.26)
(d2.26)
Konzervatív erő. Helyzeti energia formák.
Def.: Konzervatív erőnek nevezzük azt az erőt, amely egy skalár függvény hely szerinti deriváltjának (–1)-szereseként kiszámítható.
Def.: Helyzeti (potenciális) energiának (potential energy, jele: Eh, vagy Ep) nevezzük azt a helytől és a TP tömegétől függő skalár mennyiséget, amelynek a helykoordináta szerinti differenciálhányadosának (–1)-szerese erőt szolgáltat.
Egysége: kg m2 s-2 =
N m = J (Joule):
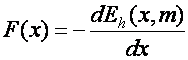 (d2.27)
(d2.27)
a. Nehézségi erőtérbeli helyzeti energia. Az m tömegű TP
helyzeti energiája a Föld felszíne közelében, a z=0 szinttől mért
z=h
magasságban
![]() . (d2.28). Ez egyenlő az un. emelő erő (
. (d2.28). Ez egyenlő az un. emelő erő (![]() ) munkájával.
) munkájával.
b. Rugalmas erő "erőterének" a
helyzeti energia. Az m tömegű TP helyzeti energiája a
rugalmas erő "erőterében" az egyensúlyi helyzettől xo helyen
![]() . (d2.29)
. (d2.29)
c. Az m1 tömegű
TP gravitációs erőterében az m2 tömegű
TP helyzeti energiája. Az m2 tömegű
TP helyzeti energiája az m1 tömegű
TP gravitációs erőterében ro távolságban
a végtelen távoli helytől mérve
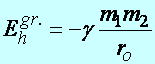 (d2.30)
(d2.30)
Pontrendszer mechanikája. Külső, belső erők. Impulzus. Impulzustétel. Impulzus megmaradás tétele.
Def.: Pontrendszer a kettő, vagy ennél több tömegpont együttese
Megjegyzés: A pontrendszer modell, az egyetlen tömegpont modellhez viszonyítva, képes figyelembe venni a valóságos testek belső mozgását, kölcsönhatását is. A rendszer szempontjából az erőket külső és belső erőkre oszthatjuk fel. Jelölje n a tömegpontok számát, i pedig a futóindexet, amely 1–től n–ig változik.
Def.:
Külső erők (az i–dik tömegpontra ható külső erők eredője, jele: ![]() ) a pontrendszerhez nem tartozó tömegpontok hatásai a
pontrendszer tagjaira.
) a pontrendszerhez nem tartozó tömegpontok hatásai a
pontrendszer tagjaira.
Def.:
Belső erők (az i–dik tömegpontra ható belső erők eredője, jele: 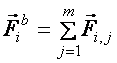 ) a pontrendszer tagjainak egymásra gyakorolt hatása.
) a pontrendszer tagjainak egymásra gyakorolt hatása.
Tétel:
Az i–dik tömegpont mozgásegyenlete előző fogalmakkal az
impulzussal megadva:
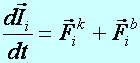 (d2.15)
(d2.15)
Def.:
A pontrendszer impulzusa (jele:
![]() ) egyenlő a pontrendszer tagjai impulzusának (vektori)
összegével.
) egyenlő a pontrendszer tagjai impulzusának (vektori)
összegével.
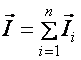 (d2.16)
(d2.16)
Tétel:
(Pontrendszer impulzustétele) A pontrendszer impulzusának idő
szerinti első differenciál hányadosa egyenlő a külső erők eredőjével.
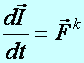 (d2.17)
(d2.17)
Def.: Zárt rendszernek nevezünk egy pontrendszert, ha a külső erők eredője zérus.
Tétel: (Pontrendszerre vonatkozó impulzus megmaradás tétele) Zárt pontrendszer impulzusa állandó.
Megjegyzések: Belső erők a pontrendszer impulzusát nem változtatják meg. Alkalmazható a megmaradási tétel testek ütközésének és szétrepülésének leírására. Megfogalmazható az impulzus tétel másképpen is, ami a tömegközéppont bevezetésére ad alkalmat.
Tétel: (Pontrendszer tömegközéppont mozgásának tétele) Pontrendszer tömegközéppontja úgy mozog, mintha ott lenne a pontrendszer teljes tömege egyesítve, és rá csak a külső erők eredője hatna:
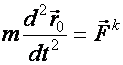 ahol
ahol
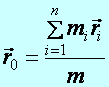 (d2.18)
(d2.18)
A mechanika megmaradási tételei
Tétel:
Mechanikai energia megmaradás tétele, (MEMT):
Konzervatív erőtérben, (amikor az m tömegű TP–ra ható erők
eredője konzervatív), a TP mozgási (Em)
és helyzeti (Eh)
energiájának összege (mechanikai energia összeg), a mozgás folyamán
állandó:
![]() (d5.11)
(d5.11)
Megjegyzések: A mechanikai energia megmaradás tételéhez a dinamika alapegyenletének felhasználásával lehet jutni a munkatételen keresztül. Ez az egyenlet könnyebben kezelhető (csak szorozni, összeadni kell), mint a dinamika alapegyenlete, mégis általa értékes felvilágosítást kaphatunk a mozgásról anélkül, hogy a mozgásegyenleteket megoldanánk.
Def.: Zárt rendszernek nevezünk egy pontrendszert, ha a külső erők eredője zérus.
Tétel:
(Pontrendszerre vonatkozó impulzus megmaradás tétele) Zárt
pontrendszer impulzusa állandó:
azaz, ha ![]() , akkor
, akkor
![]()
Megjegyzések: Belső erők a pontrendszer impulzusát nem változtatják meg.
Def.: Zárt rendszernek (teljesen) nevezünk egy pontrendszert, ha a külső erők eredője zérus és ha a külső erők nyomatékainak eredője is zérus.
Tétel:
(Pontrendszer impulzusnyomaték megmaradásának tétele) Ha a
tömegpontok között ható belső erők centrálisak, és a külső erők
nyomatékainak az eredője zérus, akkor a pontrendszer impulzusnyomatéka
állandó:
azaz, ha ![]() , akkor
, akkor
![]()
Mechanikai feladat megoldásának lépései az anyagi pont és a pontrendszer mechanikájának teljes ismeretében:
1. Több testből álló együttes esetében dönteni kell, hogy külön tekintem az egyes testeket, vagy egyetlen pontrendszerként lehet az egészet kezelni.
2. Szükséges-e a testek pályáját kiszámolni, vagy csak elegendő egy pontban ismert sebesség adatból egy másik pontbeli sebesség adatra következtetni, (azaz a mozgásegyenletet kell-e felírni, vagy valamelyik mechanikai energia formát tartalmazó tételt).
3. Az összes erő ismeretében ellenőrzöm azt, hogy a külső erők eredője zérus-e, (alkalmazható–e a pontrendszerre vonatkozó impulzus tétel).
4. Az összes erő figyelembe vétele után elemzem, hogy a testrendszerre ható erők eredője konzervatív-e, vagy disszipatív (alkalmazható-e a MEMT, vagy csak a MT, ill. az ÁET a pontrendszerként modellezett testrendszerre).
5. Ha az előző feltétel nem teljesül, akkor az egyes testek esetében elemzem, hogy külön–külön a rájuk ható erők konzervatívak-e, vagy disszipatívak (alkalmazható-e a MEMT, vagy csak a MT, ill. az ÁET az egyes tömegponttal modellezett testre).