MECHANIKA - ELŐADÁS ANYAG
Anyagi pont, koordináta rendszer
A legegyszerűbb mozgások
Egyenes vonalú egyenletes mozgás.
Egyenes vonalú egyenletesen
változó mozgás.
A sebesség és a gyorsulás legáltalánosabb
megadása:
Körpályán történő egyenletes mozgás.
Körpályán történő egyenletesen
változó mozgás.
Lineáris csillapítatlan harmonikus rezgés.
Anyagi pont, koordináta rendszer.
Az anyagi pont fogalom „megalkotását” a mozgó test és a pályájának mérete közötti arány extrapolálása „indukálta”. A következő példákban ez az arány közel azonos, azaz a mozgó test „pontszerű” a pálya méretéhez képest (Vigyázat nem a test pontszerű!)
|
Esemény |
A test és a pályahossz aránya |
|
Autó megy Pécsről Budapestre. |
1/105 |
|
Otthonról bemegyek az egyetemre |
1/104 |
|
Föld kering a Nap körül |
1/104 |
|
Eldobunk egy diszkoszt |
1/103 |
Ezek alapján célszerűnek látszik a valódi
testek modellezésére a legegyszerűbb geometriai "alakzatot", a geometriai
pontot használni. Azt pedig, hogy ez nem csak egy pont, hanem ott egy "test"
van, a következő kifejezéssel hangsúlyozzuk: anyagi pont (rövidítve:
AP).
A másik test modellezését, amelyhez képest az általunk vizsgált test
változtatja helyzetét (mozog) Descartes–féle derékszögű koordináta
rendszer formájában tesszük meg. Az útvonal modellje pedig, követve a
geometriai fogalmakat, a geometriai vonal lesz.
A mechanikában a teret háromdimenziósnak fogjuk fel, ezért ennek a leírására
egy háromtengelyű koordináta rendszert fogunk használni. Az AP helyét ezek
után helyvektorral adhatjuk meg (jele
![]() ). Komponensei leggyakrabban a természetes koordináták: x,
y, z.
). Komponensei leggyakrabban a természetes koordináták: x,
y, z.
Def.: A Descartes–féle derékszögű, jobbsodrású koordináta rendszer a térben három, páronként egymásra merőleges, közös origójú számegyenesből (tengelyekből) áll; az első az x, a második az y, a harmadik a z tengely; sorrendjük az óramutató járásával ellentétes, vagy jobbcsavart alkot.
Def.:
A helyvektor a koordináta rendszer origójából a kérdéses pontba
mutató, irányított szakasz. Jele:
![]() . Hossza: |r|, vagy csak r. A helyvektor
koordinátái a derékszögű koordináta rendszerben rendezett számhármasok.
. Hossza: |r|, vagy csak r. A helyvektor
koordinátái a derékszögű koordináta rendszerben rendezett számhármasok.
Def.:
A természetes koordináták a Descartes–féle koordináta rendszerben egy
P pontnak, illetve az oda mutató,
![]() helyvektor
végpontjának a tengelyekre eső vetületeinek az origótól mért távolsága. A
helyvektor–idő függvény (jele:
helyvektor
végpontjának a tengelyekre eső vetületeinek az origótól mért távolsága. A
helyvektor–idő függvény (jele:
![]() ) az anyagi pont mozgását megadó koordináta–idő függvények
(x(t), y(t), z(t)) tömör jelölésére szolgál.
) az anyagi pont mozgását megadó koordináta–idő függvények
(x(t), y(t), z(t)) tömör jelölésére szolgál.
Összefoglalva Az anyagi pont helyzetének ismerete azt jelenti, hogy ismerjük helyvektorát azaz három, megfelelő sorrendben megadott adatot, mozgásának ismerete pedig azt jelenti, hogy ismerjük a helyvektor–idő függvényét (amely végpontja szemléletesen a pályát futja be), azaz ismerünk három, megfelelő sorrendben megadott helykoordináta–idő függvényt, tehát
![]() (d1.1)
(d1.1)
A legegyszerűbb mozgások
A valódi testek valódi mozgásai végtelen sokfélék. Csak véges számú esetet tudunk leírni és a valóságos eseteket ezekkel próbáljuk közelíteni. Csak a legegyszerűbb mozgásokról beszélünk, amelyek a legegyszerűbb térgörbék és a legegyszerűbb időbeliségek kombinációi:
|
Legegyszerűbb térgörbék: |
egyenes, |
|
|
kör |
|
Legegyszerűbb időbeliség |
egyenletes |
|
|
egyenletesen változó |
|
|
harmonikus rezgés. |
Ezek alapján a legegyszerűbb mozgások a
következők:
Egyenes vonalú egyenletes mozgás
Egyenes vonalú egyenletesen változó mozgás
Egyenletes körmozgás
Egyenletesen változó körmozgás
Harmonikus rezgőmozgás egyenes mentén
Harmonikus rezgőmozgás körív mentén
Egyenes vonalú egyenletes mozgás
Def.: Időben egyenletes az anyagi pont mozgása, ha egy útszakasz megtétele során (bárhogy is választva meg annak megtételéhez szükséges teljes időtartam egyenletes beosztását), azonos kis időtartamok alatt azonos utakat tesz meg.
Megjegyzések: Ez a definíció egyébként annyit is jelent, hogy az AP által megtett út egyenesen arányos az eltelt idővel, azaz s ~ t, vagy x ~ t. Az arányosság azt is jelenti, hogy az s/t, illetve az x/t hányados állandó. Ez az állandó jellemző lehet az adott AP mozgására, mert arra utal, hogy ugyanazt az utat hamarabb (gyorsabban, sebesebben) teszi meg az egyik AP, mint a másik, ha az ő mozgását leíró ilyen hányados nagyobb. Ezt a hányadost ezért célszerű fizikai mennyiség "rangjára" emelni.
Def.:
A sebesség (velocitas jele:
![]() )
a hosszúság (az út) és az idő hányadosával definiált fizikai mennyiség.
)
a hosszúság (az út) és az idő hányadosával definiált fizikai mennyiség.
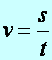 (d1.2)
(d1.2)
Megjegyzések: A sebesség definíciójából következik, hogy az származtatott mennyiség, és így a mértékegységének származtatása is ilyen úton történik, tehát egysége a méter/secundum, röviden m/s.
A következő testek a mozgásuk adott szakaszán
jó közelítéssel teljesítik ezt:
- a 100 méteres síkfutó a start után 20 métertől 100 méterig,
- közlekedő vonat hosszú, nyílt pályán,
- esőcsepp a talajhoz közeli 100 méteren,
- meglökött kocsi a vízszintes légpárnás pályán,
- olajcsepp a Millikan–féle kísérletben, stb.
Sebesség mérése:
Egy valóságos test mozgásának minősítését abból a szempontból, hogy
közelítőleg egyenletes mozgást végez-e, a definíciót felhasználva a
következőképpen végezhetjük el. A pályájához illesztünk egy skálát,
felvesszük a beosztás kezdőpontját. Egy eszközzel (pl. metronóm) időben
periódikusan ismétlődő jeleket állítunk elő és ezekben az "időpontokban"
(egyenlő időközönként) leolvassuk a test helyzetét (egy kijelölt pontjának a
helyzetét). Ezután ábrázoljuk az összetartozó helykoordináta-idő adatokat
grafikonon. Ha a mérési eredményekre, a regresszió számításnak megfelelően,
lehetséges egyenest illeszteni, akkor azt mondhatjuk, hogy a test mozgása
egyenletes volt. Az egyenes meredeksége adja a sebesség értékét.
Elkészíthetők sebesség mérő célkészülékek, amelyek olyan fizikai törvényszerűségeken alapulhatnak, amelyek esetében egy közvetlenül mérhető mennyiség valamilyen kapcsolatban van a mozgás sebességével. Pl. a torlónyomás a sebesség négyzetével arányos, ezért a nyomásmérőt sebesség mérés céljából négyzetes skálával kell ellátni.
Egyenes vonalú egyenletesen változó mozgás
Def.: Időben egyenletesen változó az anyagi pont mozgása, ha egy útszakasz megtétele során (bárhogy is választva meg annak megtételéhez szükséges teljes időtartam egyenletes beosztását), azonos időtartamok alatt a sebességének a megváltozása azonos mértékű.
Megjegyzések: Ez a definíció egyébként annyit is jelent, hogy az AP sebessége egyenesen arányos az eltelt idővel, azaz v ~ t. Az arányosság azt is jelenti, hogy a v/t hányados állandó. Ez az állandó jellemző lehet az adott AP mozgására, mert megadja, hogy ugyanazon időtartam alatt az egyik esetben az AP nagyobb sebességre tett szert, mint a másik esetben, ha a mozgását leíró ilyen hányados nagyobb. Ezt a hányadost ezek után célszerű fizikai mennyiség "rangjára" emelni.
Def.:
A gyorsulás (acceleratio jele:
![]() )
a sebesség és az idő hányadosával definiált fizikai mennyiség.
)
a sebesség és az idő hányadosával definiált fizikai mennyiség.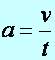 (d1.3)
(d1.3)
Megjegyzések:
A gyorsulás definiciójából következik, hogy az származtatott mennyiség, és
így a mértékegységének származtatása is ilyen úton történik, tehát egysége a
méter/secundum2,
röviden m/s2.
Az egyenletesen változó mozgás során a megtett út- az idő négyzetével
arányosan változik,
![]() .
.
Az egyenletesen változó mozgás kinematikai leírására, amennyiben xo kezdő
helykoordinátájú helyről, vxo kezdősebességgel
indul a test és ax a
gyorsulása, akkor a helykoordináta-idő, x(t) és a sebesség-idő, v(t)
függvények a következők:
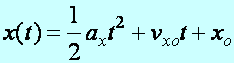 (d1.4)
(d1.4)
![]() (d1.5)
(d1.5)
A következő testek a mozgásuk adott szakaszán
jó közelítéssel teljesítik ezt:
- egyenletesen behavazott domboldalon szánkóval lecsúszunk,
- az első sebességfokozatban autóval azonos gázpedál nyomás mellett
elindulunk,
- 2–3 méter magasból leejtjük az acélgolyót,
- ferde légpárnás pályán elengedjük a kocsit, stb.
Gyorsulás mérése:
Egy valóságos test mozgásának minősítését abból a szempontból,
hogy közelítőleg egyenletesen változó mozgást végez-e, a definíciót
felhasználva a következőképpen végezhetjük el. A pályájához illesztünk egy
skálát, felvesszük a beosztás kezdőpontját (az origót) egy eszközzel (pl.
metronóm) időben periódikusan ismétlődő jeleket állítunk elő és ezekben az
"időpontokban" (egyenlő időközönként) leolvassuk a test helyzetét (egy
kijelölt pontjának a helyzetét). Egy–egy időtartamra átlagsebességet
számolunk. Ezután ábrázoljuk az időtartamok felében az oda tartozó
átlagsebesség értékeket grafikonon. Ha a mérési eredményekre, a regresszió
számításnak megfelelően, lehetséges egyenest illeszteni, akkor azt
mondhatjuk, hogy a test mozgása egyenletesen változó volt. Az egyenes
meredeksége adja a gyorsulás értékét.
Elkészíthetők gyorsulás mérő célkészülékek, amelyek olyan fizikai törvényszerűségeken alapulhatnak, amelyek esetében egy közvetlenül mérhető mennyiség valamilyen kapcsolatban van a gyorsulással. Ilyen gyorsulás mérő eszköz egy fonálinga (felakasztott fonálon egy nehezék, vagy vízzel teli zárt üvegtartály aljára fonallal lekötött parafadugó), amely annak a testnek a gyorsulásától függően tér ki az eredeti helyzetéből, amelyikre rögzítették.
A sebesség és a gyorsulás legáltalánosabb megadása:
Def.:
A pillanatnyi sebesség (vektor) (jele:
![]() ) a helyvektor idő szerinti első differenciálhányadosa:
) a helyvektor idő szerinti első differenciálhányadosa:
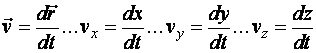 (d1.6)
(d1.6)
Def.:
A pillanatnyi gyorsulás (vektor) (jele:
![]() ) a sebességvektor idő szerinti első, vagy a helyvektor
idő szerinti második differenciálhányadosa:
) a sebességvektor idő szerinti első, vagy a helyvektor
idő szerinti második differenciálhányadosa:
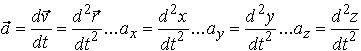 (d1.7)
(d1.7)
Megjegyzések: A pillanatnyi sebesség Newton óta értelmezett az általa bevezetett (feltalált) differenciál- és integrálszámítás alapján. A pillanatnyi sebesség a helyvektor differenciálásával képes kódolni nemcsak a sebesség nagyságát (ami az út idő szerinti differenciálhányadosával egyenlő), hanem a mozgás irányát is azzal, hogy a differenciálás során kapott vektor mindig a pálya érintőjébe esik és iránya a mozgás irányába mutat.
Az eddigi definíciók, mint az a körmozgás tárgyalása során kiderülhet, nemcsak az egyenes, hanem tetszőleges ívű pályán történő mozgás során is alkalmasak a megfelelő sebesség és gyorsulás vektorok (komponenseik) számítására.
Körpályán történő egyenletes körmozgás
Az AP körpályán történő egyenletes mozgásának a definíciója a körív tetszőleges beosztásával teljesen hasonlóan adható meg, mint az egyenes mentén bekövetkező mozgások esetében. Azonban a körmozgás leírását szögelfordulással is jellemezni lehet, ami újabb származtatott mennyiségekre ad lehetőséget.
Def.: : Időben egyenletes az anyagi pont körmozgása, ha egy nagyobb szögelfordulás során (bárhogy is választva meg az annak megtételéhez szükséges teljes időtartam egyenletes beosztását), azonos időtartamok alatt azonos a szögelfordulás.
Megjegyzések:
Ez a definició egyébként annyit is jelent, hogy az AP által a körív mentén
megtett út is és a szögelfordulás is egyenesen arányos az eltelt idővel,
azaz i
~
t, és
j
~
t.
Az arányosság azt is jelenti,
hogy az i/t, illetve az
j/t
hányados állandó. Ezt a két
állandót fizikai mennyiségként értelmezzük
Def.:
A kerületi sebesség (jele:
![]() ) az ívhosszúság (i) és az idő hányadosával
definiált fizikai mennyiség. Egysége: m/s.
) az ívhosszúság (i) és az idő hányadosával
definiált fizikai mennyiség. Egysége: m/s.
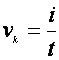 (d1.8)
(d1.8)
Def.:
A szögsebesség (jele:w)
a szögelfordulás (j)
és az idő hányadosával definiált fizikai mennyiség. Egysége: s-1.
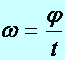 ,
(d1.9) másrészt
,
(d1.9) másrészt
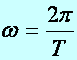 , (d1.10)
, (d1.10)
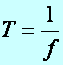 (d1.11)
(d1.11)
Megjegyzés:
A kerületi sebesség és a szögsebesség között fennáll a következő
összefüggés:
![]() (d1.12)
(d1.12)
Tétel:
Az egyenletes körmozgás, gyorsuló mozgás, a gyorsulás
iránya a kör középpontja felé mutat (centripetális,
![]() ), nagysága pedig a következőképpen számolható ki:
), nagysága pedig a következőképpen számolható ki:
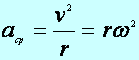 (d1.13)
(d1.13)
A következő testek a mozgásuk adott szakaszán
jó közelítéssel teljesítik ezt:
- a körhinta egy ülésének mozgása a menet időtartamának félidejében,
- a lemezjátszó lemezén egy porszem lejátszás közben.
- a Föld körül egy űrhajó,
- az áramfejlesztő forgórészének egy pontja, stb.
Körpályán történő egyenletesen változó körmozgás
Def.: Időben egyenletesen változó az anyagi pont körmozgása, ha azonos időtartamok alatt a kerületi sebességének és ezzel a szögsebességnek a megváltozása azonos mértékű.
Megjegyzések:
Ez a definició egyébként annyit is jelent, hogy az AP által a körív mentén a
kerületi sebesség is és a szögsebesség is egyenesen arányos az eltelt
idővel, azaz
![]() és
és
![]() .
.
Az arányosság azt is jelenti, hogy az
![]() , illetve az
, illetve az
![]() hányados
állandó. Ezt a két állandót ezek után fizikai mennyiségként értelmezzük.
hányados
állandó. Ezt a két állandót ezek után fizikai mennyiségként értelmezzük.
Def.:
A kerületi (érintőleges, v. tangenciális) gyorsulás (jele:
![]() ) a kerületi sebesség (
) a kerületi sebesség (![]() ) és az idő hányadosával definiált fizikai mennyiség.
Egysége: m/s2.
) és az idő hányadosával definiált fizikai mennyiség.
Egysége: m/s2.
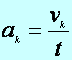 (d1.14)
(d1.14)
Def.: A szöggyorsulás (jele:b) a szögsebesség (w) és az idő hányadosával definiált fizikai mennyiség. Egysége: s-2.
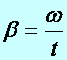 (d1.15)
(d1.15)
Megjegyzés: A kerületi gyorsulás és a szöggyorsulás között fennáll a következő összefüggés:
![]() (d1.16)
(d1.16)
A következő testek a mozgásuk adott szakaszán
jó közelítéssel teljesítik ezt:
- a körhinta egy ülésének mozgása közvetlenül elindulás után,
- a személygépkocsi kanyarban fékezés közben
- a kerekes kút hajtókarja, miközben a vödör szabadon elindul lefelé, stb.
Tétel:
Az egyenletesen változó körmozgás olyan gyorsuló mozgás,
amelynél a gyorsulás vektor (![]() ) iránya a körív homorú oldala felé mutat, és amelynek az
érintőleges, v. tangenciális komponensének (
) iránya a körív homorú oldala felé mutat, és amelynek az
érintőleges, v. tangenciális komponensének (![]() ), valamint a görbületi sugár irányú, normális,
v. centripetális komponensének (
), valamint a görbületi sugár irányú, normális,
v. centripetális komponensének (![]() ), a nagyságát pedig a következőképpen számolhatjuk ki:
), a nagyságát pedig a következőképpen számolhatjuk ki:
![]() (d1.17) továbbá
(d1.17) továbbá
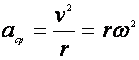 (d1.18)
(d1.18)
azaz
![]() (d1.19)
(d1.19)
Megjegyzés:
Az egyenletesen változó körmozgás során a megtett út- (az ív hossza és a
szögelfordulás) az idő négyzetével arányosan változik,
![]() .
.
Az egyenletesen változó körmozgás kinematikai leírására, amennyiben
![]() kezdő helykoordinátájú helyről,
kezdő helykoordinátájú helyről,
![]() kezdő szögsebességgel indul a test és
b
a szöggyorsulása, akkor a szögelfordulás-idő,
kezdő szögsebességgel indul a test és
b
a szöggyorsulása, akkor a szögelfordulás-idő,
![]() és a szögsebesség-idő,
és a szögsebesség-idő,
![]() függvények a következők:
függvények a következők:
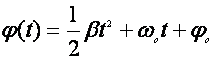 (d1.20)
(d1.20)
![]() (d1.21)
(d1.21)
Egyenes mentén történő harmonikus rezgőmozgás
Def.: Lineáris (csillapítatlan) harmonikus rezgőmozgás az AP olyan mozgásformája, amely során úgy mozog, hogy egy O vonatkoztatási ponttól számított kitérése (x) az egyenes mentén két irányban az időnek harmonikus (szinusz, koszinusz) függvénye:
![]() (d1.22)
(d1.22)
ahol
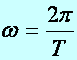 , (d1.23)
, (d1.23)
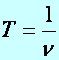 (d1.24)
(d1.24)
továbbá:
A -
amplitúdó,
w
-
körfrekvencia,
T -
rezgésidő, vagy periódusidő,
n
-
rezgésszám, vagy frekvencia,
![]() -
fázis,
-
fázis,
a
-
kezdőfázis.
Megjegyzés: A lineáris
(csillapítatlan) harmonikus rezgőmozgás sebesség (![]() ) és gyorsulás (
) és gyorsulás (![]() ) időfüggvényei a következők:
) időfüggvényei a következők:
![]() (d1.25)
ahol
(d1.25)
ahol
![]() ,
(d1.26)
,
(d1.26)
![]() (d1.27)
(d1.27)
ahol
![]() , (d1.28)
, (d1.28)
Ezekből látszik, hogy a gyorsulás a kitéréssel arányos és ellentétes irányú.
A következő testek a mozgásuk adott szakaszán
jó közelítéssel teljesítik ezt:
- függőleges gumiszalagra akasztott testet lehúzunk, majd elengedünk,
- úszót (horgászati) lenyomunk a vízben, majd elengedjük,
- ugródeszka szabad vége kis lehajlítás és elengedés után, stb.
Laboratóriumi mérési gyakorlatok
D1. Alapvető mérések az anyagi pont kinematikájából:
1. A HOSSZÚSÁG MÉRÉSE
D1.1. Alapvető kérdések a hosszúság mérés terén
D1.2. Hosszúság mérés speciális esetekben
2. AZ IDŐTARTAM MÉRÉSE
D1.3. Alapvető kérdések az időtartam mérés terén
D1.4. Időtartam mérése speciális esetekben
3. EGYENES VONALÚ EGYENLETES MOZGÁS VIZSGÁLATA. SEBESSÉG MÉRÉSE
D1.5. Ferde Mikola-féle csőben mozgó buborék sebességének mérése. Az s(t) függvénykapcsolat és a v meghatározása.
D1.6 Vízszintes légpárnás pályán mozgó kiskocsi sebességének mérése. Az s(t) függvénykapcsolat és a v meghatározása.
4. EGYENES VONALÚ EGYENLETESEN VÁLTOZÓ MOZGÁS VIZSGÁLATA. GYORSULÁS MÉRÉSE
D1.7. Az eső acélgolyó gyorsulásának mérése. Az s(t) függvénykapcsolat és a g meghatározása.
D1.8. Ferde légpárnás pályán mozgó kiskocsi gyorsulásának mérése. A v(t), az s(t), az a(α) kapcsolat és a g meghatározása.
5. REZGŐ MOZGÁS VIZSGÁLATA
D1.9. A Borda-féle inga lengésideje és a hossza közti kapcsolat vizsgálata. A g meghatározása.
D1.10. Anyagi pont csillapítatlan és csillapított harmonikus rezgésének számítógépes modellezése.