Az elemi töltés létezésére vezető tapasztalatok. Az elektron töltése

Az elektron fajlagos töltése J.J.Thomson kísérlet alapján

Hőmérsékleti sugárzás. Planck-féle sugárzási törvény

Külső fotoeffektus. Einstein egyenlet.

Az energia kvantumos gondolata. H-atom színképe. Atomszínképek.

 

Az elemi töltés létezésére vezető tapasztalatok. Az elektron töltése

 

Az elektrolízis Az elektrolitokban (savak, lúgok, sók vizes oldatai) a beléjük merülő elektródákon keresztül áram folyik; gáz, vagy szilárd anyag válik ki.

Faraday tapasztalati törvényei:

Az m tömegű anyag kiválasztásakor:      (a1.1)

 

A molnyi mennyiség kiválasztásához 96500 C töltés szükséges.

Létezik egy legkisebb töltés: 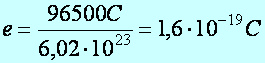       (a1.2)

 

 

A Millikan-féle kísérlet (1906): (1868-1953):

Kísérlet leírása: Vízszintes síkkondenzátor közé olajcseppeket porlasztva, a feszültséggel szabályozni lehet, melyik ne essen le.

Kvalitatív értelmezés: A porlasztáskor, elektrosztatikus megosztás során adott töltés mennyiségre tett szert az olajcsepp.

Kvantitatív következtetés: Ha az olajcsepp lebeg, akkor súlyával (G=mg) azonos nagyságú az elektromos tér hatása (F=QE). Mindegyik olajcsepp összes töltése, egész számú többszöröse egy értéknek, az elemi töltésnek (e). Az elektronok mozgékonyságának feltételezésével, feltételezhető, hogy ez az érték az elektron töltése lehet.

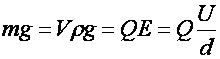   eredmény      (n=1,…i.)    (a1.3)

 

Tétel: A töltés kvantuma, az elemi töltés értéke:             (a1.4)

 

 

Az elektron fajlagos töltése J.J. Thomson kísérlete alapján

 

Kísérlet leírása: J.J. Thomson (1856-1940) (1897) Egy katódsugárcsőben a katódot izzítjuk. Az anód-katód között ismert gyorsító feszültséget (U) alkalmazunk, ami mérhető, anód után kirepülő töltött részecskék (elektronok?) ismert (tekercs árama, mérete, mágneses szuszceptibilitása mérhető) homogén mágneses térbe (B) kerülnek, körpályán mozognak, a körpálya sugara (R) mérhető.

Kvalitatív értelmezés: A változtatott elektromos térerősség és a mágneses térerősség értékekből, megállapítható a mozgó töltött rész neme: negatív, az izzó katódból elektronok lépnek ki.

Kvantitatív következtetés:

A jelenség leírására két törvényszerűség, két egyenlet írható fel a mérésadatokból A két egyenletből meghatározható két ismeretlen, a részecske sebessége (v) és a fajlagos töltése (q/m):

Dinamika alapegyenlete: 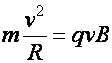                 Þ 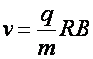               (a1.5)

 

Munkatétel az elektromos térre 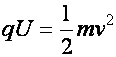               (a1.6)

 

Þ 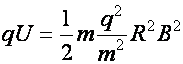     a fajlagos töltés: 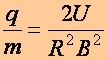         (a1.7)

 

 

Tétel: A Millikan-féle kísérletből az elemi töltés értékét felhasználva az elektron tömege:

 

                 (a1.8)

 

 

Hőmérsékleti sugárzás. Planck-féle sugárzási törvény

 

1. Wien-féle eltolódási törvény (1893):

         ,      (a1.9)

 

2. Stefan-Boltzmann-törvény:    (a1.10)

 

                  (a1.11)

 

3. Planck-féle sugárzási törvény (1900) Planck (1858-1947):

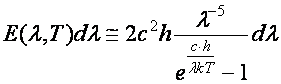                   (a1.11)

 

 

              (15.11)                  ahol a Planck-állandó, (energiakvantum)

 

                    (a1.12)

 

Külső fotoeffektus. Einstein egyenlet

 

Kísérlet leírása: Alkalmazzunk egy két elektródás vákuumcsőre, amelynek a katódja pl. cinkből legyen. Mérjük érzékeny árammérővel az áramkörben az áramot akkor, ha nem esik fény a katódra és akkor is, amikor különböző színű (vörös, zöld, kék, ibolya) és intenzitású fény bocsátunk. Tapasztalat: sötétben nincs áram, vörösnél szintén nincs, akármilyen erős is a vörös fény. Nagyon gyenge kék, sőt még inkább ibolya fény esetében van áram és nő az intenzitással.

Kvalitatív értelmezés: Feltesszük, hogy ebben az esetben is elektronok lépnek ki a fémből. Azonban egy elektron kilépéséhez szükséges egy adott értékű munkavégzés (kilépési munka). Ezt a szükséges értéket az ibolya és a kék színű fény adagokban tudja fedezni, az intenzitás növelés pedig ezeknek az adagoknak a számát növeli. A vörös fényben egy adagnak a nagysága nem éri el az egy elektron kiléptetéséhez szükséges munkát.

Összefoglalva: Az anyagban kötött elektron egyszerre csak egy fotonnal lép kölcsönhatásba. A fény nem folytonosan, hanem adagokban, kvantumokban szállítja az energiát.

Kvantitatív következtetés:

Az energiakvantum (neve: foton) nagysága arányos a fény frekvenciájával:

  (a1.13)

Tétel: Einstein-féle egyenlet: ahol W jelentése kilépési munka.

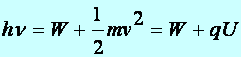         (a1.14)

 

 

Az energia kvantumos gondolata. H-atom színképe. Atomszínképek.

 

A spektroszkópiai méréseredmények: (Kirchoff, Bunsen,  ) ábrázolásánál, összevetésénél, alkalmazott „technika” az energiaszint (E) szerinti (term, T) ábrázolás. A foton energiaszintjeinek egységei a következők: aJ, eV, .

A hullámhossz-frekvencia és a hullámhossz- hullámszám kapcsolatot felhasználva:

         , ahol 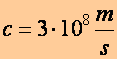        (a1.15)

 

az energia szintek értékeit a következő összefüggésekkel lehet számítani:

         , ahol 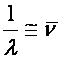   a hullámszám        (a1.16)

 

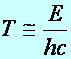
                    (a1.17)

 

A Hidrogén atom színképe

A hidrogén által kisugárzott fény látható tartományba eső vonalainak hullámhossza, frekvenciája, hullámszáma, és az adott foton energiája (aJ) és (eV) egységekben (10-18 J= aJ; 1 eV = 1,6 10-19 J= 0,16 aJ; 1 aJ = 6,25 eV; 1 aJ=50,256 103 cm-1):

Vonal jele	l (nm)	n (THz)	(cm-1)	E(aJ)	E(eV)
a	656,4	457,3	15235	0,303	1,89
b	486,3	617,3	20563	0,409	2,56
g	434,2	691,2	23031	0,458	2,86
d	410,3	731,7	24372	0,485	3,03
e	397,1	755,7	25183	0,501	3,13

 

Balmer-formula (1885). Balmer (1825-1898) próbálkozással kialakított egy képletet, amelyből mindegyik hullámhossz értéket származtatni lehet:

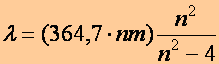  (n=3, 4, 5, 6)      (a1.18)

 

Balmer után az előzőből egy általánosabb alakot fejeztek ki, amely alapján „csoportokba lehet rendszerezni” a hidrogén későbbiek során kimért spektrumvonalait is. A teljes rendszer az „osztályozás” után a következő:

Lyman-sorozat	1906	k=1	n=2, 3, 4, 5,..
Balmer-sorozat	1885	k=2	n=3, 4, 5,..
Paschen-sorozat	1908	k=3	n=4, 5, 6,..
Brackett-sorozat	1922	k=4	n=5, 6, 7,..
Pfund-sorozat	1924	k=5	n=6, 7, 8,..

 

A Rydberg-féle képlet foglalja mindezeket egységbe: (Rydberg, 1854-1919)

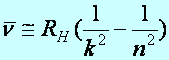
       (a1.19)